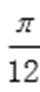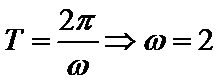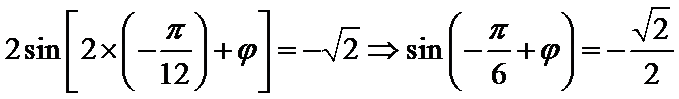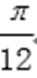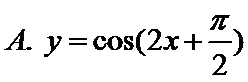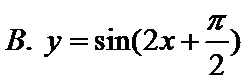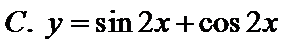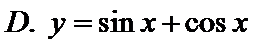三角函数的周期性及其求法
共131题

· 三角函数的周期性及其求法

三角函数的周期性及其求法
共131题

热门试卷

X 查看更多试卷

题型：填空题

填空题 · 5 分

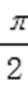
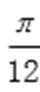
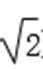
8．已知函数f(x)＝2sin(ωx＋φ)(ω＞0，|φ|＜)的最小正周期为π，且它的图象过点(－，－ )，则φ的值为．

正确答案

－

解析

由题意可知：函数f(x) 的最小正周期为π，

∵它的图象过点(－，－)，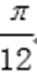

∴

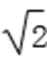
∵|φ|＜

Φ=－

考查方向

本题主要考查了三角函数图象和性质，的部分图象求解析式

解题思路

根据最小正周期为π，利用周期公式即可求出ω的值，利用图象经过点(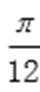－，－)，结合其范围即可求出φ的值．

易错点

把点的坐标代入到解析式求φ，一定要注意结合其范围求解

知识点

三角函数的周期性及其求法三角函数中的恒等变换应用

题型：单选题

单选题 · 5 分

7．函数f(x)＝sin(2x＋φ)的图像向左平移个单位后关于原点对称，则函数f(x)在区间上的最小值为(　　)

正确答案

解析

f(x)向右平移的函数记为g(x)= sin[2(x+)＋φ]= sin[2x+＋φ]，因为图像关于原点对称，所以g(x)为奇函数，φ=-，所以f(x)＝sin(2x - ) ,因为x0, ] , 2x - ,，由图象可知，最小值为－，选择答案A.

考查方向

三角函数图像的平移,对称问题,函数的单调性与最值问题。

解题思路

先平移，然后根据图像关于原点对称求解φ，再利用函数的单调性求最小值

易错点

1、本题易在左右平移时发生错误，易忽视x的系数；2、关于原点对称不理解；函数的基本性质理解不到位。

知识点

三角函数的周期性及其求法正弦函数的单调性

题型：单选题

单选题 · 5 分

4.下列函数中，最小正周期为且图象关于原点对称的函数是（）

正确答案

解析

对于选项A，因为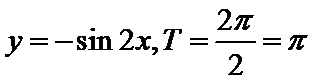，且图象关于原点对称故选 A选项.

考查方向

本题主要考察三角函数的性质等知识，意在考察考生的基础知识。

解题思路

先将选项化简后利用三角函数的周期和奇偶性判断即可。

易错点

利用诱导公式化简时没有注意奇偶导致出错；不会利用辅助角公式化简C,D选项。

知识点

三角函数的周期性及其求法三角函数中的恒等变换应用

题型：简答题

简答题 · 13 分

已知函数

（本小题满分13分，（1）小问7分，（2）小问6分）

19.求的最小正周期和最大值；

20.讨论在上的单调性.

第(1)小题正确答案及相关解析

正确答案

最小正周期为，最大值为；

解析

试题分析：三角函数问题一般方法是把函数转化为一个角，一个函数，一次式，即为形式，然后根据正弦函数的性质求得结论，本题利用诱导公式、倍角公式、两角差的正弦公式可把函数转化为，这样根据正弦函数性质可得（1）周期为，最大值为．

试题解析：（1）

因此的最小正周期为，最大值为.

考查方向

三角函数的恒等变换，周期，最值，考查运算求解能力．

解题思路

三角函数的性质由函数的解析式确定，在解答三角函数性质的综合试题时要抓住函数解析式这个关键，在函数解析式较为复杂时要注意使用三角恒等变换公式把函数解析式化为一个角的一个三角函数形式，然后利用正弦（余弦）函数的性质求解，三角函数的值域．

易错点

三角函数化简

第(2)小题正确答案及相关解析

正确答案

在上单调递增；在上单调递减.

解析

试题分析：由已知条件得，而正弦函数在和上分别是增函数和减函数，因此可得单调区间．

试题解析：当时，有，从而

当时,即时，单调递增，

当时,即时，单调递减，

综上可知，在上单调递增；在上单调递减.

考查方向

三角函数的恒等变换，单调性，考查运算求解能力．

解题思路

三角函数的性质由函数的解析式确定，在解答三角函数性质的综合试题时要抓住函数解析式这个关键，在函数解析式较为复杂时要注意使用三角恒等变换公式把函数解析式化为一个角的一个三角函数形式，然后利用正弦（余弦）函数的性质求解，三角函数的值域、三角函数的单调性也可以使用导数的方法进行研究．

易错点

函数单调性的整体方法

题型：单选题

单选题 · 5 分

8．函数满足，则的值为（）

正确答案

解析

因为，所以该图象的周期为，所以当,k=0,1,2……时，该函数满足，因为，所以的值为

考查方向

三角函数的对称性；三角函数图象的特征

解题思路

根据f(x)的对称性判断

易错点

不理解的意思

知识点

三角函数的周期性及其求法正弦函数的图象

继续学习学习下一知识点

下一知识点 : 正弦函数的图象

百度题库 > 高考 > 理科数学 > 三角函数的周期性及其求法

扫码查看完整答案与解析