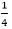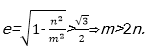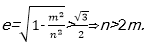- 与长度、角度有关的几何概型
- 共26题
10.一只蚂蚁在三边边长分别为3,4,5的三角形的边上爬行,某时刻该蚂蚁距离三角形的三个顶点的距离均超过
正确答案
解析
解析已在路上飞奔,马上就到!
知识点
14.在区间


正确答案
解析
解析已在路上飞奔,马上就到!
知识点
13.在区间[-6,6],内任取一个元素xO ,若抛物线y=x2在x=xo处的切线的倾角为

正确答案
解析
解析已在路上飞奔,马上就到!
知识点
8.连掷两次骰子得到的点数分别为m和n,记向量a=(m,n)与向量b=(1,-1)的夹角为θ,则θ

正确答案
解析
∵cos θ=
∴P(A)=
知识点
3.在区间(0,2)内任取两个数m,n(m≠n),则椭圆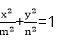
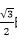
正确答案
解析
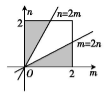
如图,m,n的取值在边长为2的正方形中.
当m>n时,焦点在x轴上,
椭圆离心率
当m<n时,焦点在y轴上,
椭圆离心率
故满足条件的m,n为图中阴影部分,
则所求概率
知识点
2.如图是某路段从晚上8点到第二天6点监控拍到的经过的车辆数量(单位:台)的茎叶图,则数据落在区间[10,20)内的概率为( ).
正确答案
解析
因为共有10个样本数据,数据落在区间[10,20)内的有2个人,所以所求概率为
知识点
16.设实数a,b均为区间[0,1]内的随机数,则关于x的不等式x2+ax+
正确答案
解析
不等式x2+ax+
关于x的不等式x2+ax+




知识点
19.已知袋内有标有1~6数字的小球6个,球除标号不同外完全相同,甲、乙两人玩“摸球赢枣”的游戏,由丙做裁判,游戏规定由丙从袋中有放回的摸三次球,记第1、2、3次摸到的球的标号分别为a,b,c,然后将所得的数代入函数f(x)=ax2+bx+c,若所得到的函数无零点,则甲输一个枣给乙,若所得到的函数有零点,则乙输四个枣给甲.
(Ⅰ)记函数的零点的个数为,求的分布列和数学期望;
(Ⅱ)根据两人得枣的数学期望,该游戏公平吗?若不公平,谁吃亏?
正确答案
(Ⅰ)解:ξ的可能取值为0,1,2.f(x)=ax2+bx+c的判别式Δ=b2-4ac,
当Δ=0时,b为偶数,b=2时,a=1,c=1;
b=4时,a=1,c=4或a=2,c=2或a=4,c=1;
b=6时,a=3,c=3,∴P(ξ=1)=
当Δ≥0时,有b≥3,b=3时,ac≤2,有3种;
b=4时,ac≤4,有9种;b=5时,ac≤6,
有14种;b=6时,ac≤9,有17种,共计43种.
∴ξ=1的情形有43-5=38种,∴P(ξ=2)=
P(ξ=0)=1- P(ξ=1)-P(ξ=2)=
∴ξ的分布列为:
数学期望 Eξ=
(Ⅱ)甲得枣的数学期望是
乙得枣的数学期望是
∴该游戏不公平,甲吃亏.
解析
解析已在路上飞奔,马上就到!
知识点
5.已知某随机变量X的概率密度函数为P(x)=
正确答案
解析
知识点
10.若


正确答案
解析
函数在R上有两个相异的极值点等价于它的导函数有两个不等的实数根,即根的判别式为大于零,可以得到

考查方向
本题主要考查概率的集合概型,导数的运用,属于难题。
解题思路
先求导,利用根的判别式判断,最后利用几何概型求解。
易错点
不理解,不会将未知内容转化成已学过的知识。
知识点
扫码查看完整答案与解析