- 正弦函数的对称性
- 共63题
1
题型:
单选题
|
将函数





正确答案
D
解析
略
知识点
正弦函数的对称性函数y=Asin(ωx+φ)的图象变换
1
题型:简答题
|
已知在



(1)求角A、B、C的大小;
(2)设函数

正确答案
(1)

解析
解析:(1)由题设及正弦定理知:
∴


当




当


∴

(2) 由(1)及题设知:
当

即

它的相邻两对称轴间的距离为 
知识点
正弦函数的单调性正弦函数的对称性三角函数中的恒等变换应用正弦定理
1
题型:
单选题
|
若函数


正确答案
C
解析
易知x=a为对称轴,所以
另解:∵x=a为对称轴,



知识点
三角函数的化简求值正弦函数的对称性
1
题型:简答题
|
设函数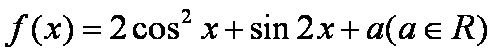
(1)求函数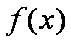
(2)当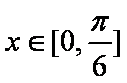
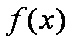
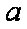
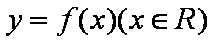
正确答案
见解析
解析
解:(1)
则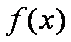
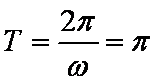
且当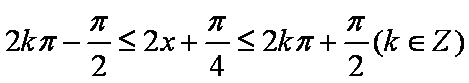
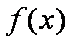
即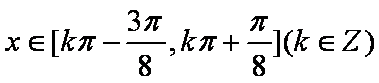
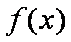
(2)当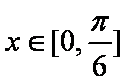
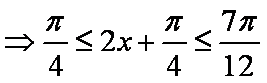
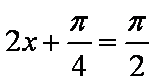
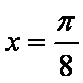
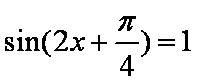
所以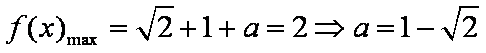
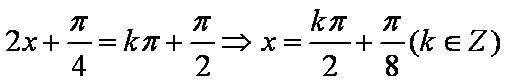
知识点
三角函数的周期性及其求法正弦函数的单调性正弦函数的对称性三角函数中的恒等变换应用三角函数的最值
1
题型:
单选题
|
已知函数


正确答案
B
解析
由函数



知识点
正弦函数的对称性三角函数中的恒等变换应用
下一知识点 : 余弦函数的图象
扫码查看完整答案与解析