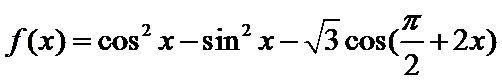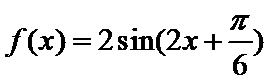- 正弦函数的对称性
- 共63题
3.在△ABC中，若
正确答案
知识点
已知
正确答案
知识点
若将函数y=2sin 2x的图像向左平移个单位长度，则评议后图象的对称轴为
正确答案
知识点
4.将函数
位，得到的函数的图像的一个对称中心为（）
A（
B（
C（
D．（
正确答案
解析
考查方向
易错点
本题易错在平移变化出错
解题思路】该题是常规题1、平移得到新函数
知识点
6. 将函数
A
B
C
D
正确答案
解析
考查方向
解题思路
1.先根据函数图像的平移得到函数
易错点
1. 误将函数
到
知识点
7．定义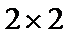
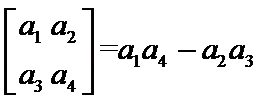
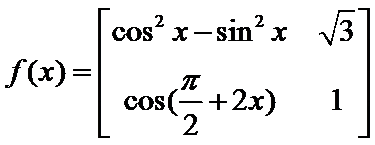
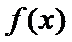
A图象关于
B图象关于直线
C在区间
D周期为
正确答案
解析
根据矩阵的定义，可以得到
所以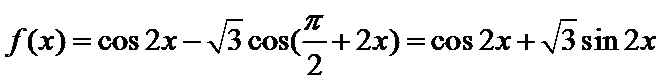
根据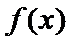
考查方向
三角函数
解题思路
先根据矩阵的定义，得到f(x)的解析式，然后根据函数的解析式判断函数的相关性质.
易错点
三角函数公式记忆混淆
知识点
4．已知函数
A关于直线
B关于直线
C关于点
D关于点
正确答案
解析
由题意得
考查方向
本题主要考查三角函数的图像和性质、诱导公式等知识，意在考查考生对于三角函数基础知识的掌握程度。
解题思路
1.先根据题中条件求出函数
2.然后利用对称中心的坐标公式求出此函数的对称中心。
易错点
1.图像平移时容易错写成
2.混淆对称中心与对称轴导致结果出错。
知识点
8.设函数
A
B
C
D
正确答案
解析
由题得周期为
考查方向
解题思路
该题首先根据周期求出
易错点
本题易错在（１）忽略Ａ为负值（２）对称中心计算错误（３）单调性不能判断
知识点
（4分）（2015•上海）已知函数f（x）=sinx．若存在x1，x2，…，xm满足0≤x1＜x2＜…＜xm≤6π，且|f（x1）﹣f（x2）|+|f（x2）﹣f（x3）|+…+|f（xm﹣1）﹣f（xm）|=12（m≥12，m∈N*），则m的最小值为 ．
正确答案
8
知识点
8．已知
A
B
C
D
正确答案
解析
三角函数相邻两对称轴正好跨度了半个周期所以
又
考查方向
解题思路
利用堆成轴间距求出周期确定
易错点
无法利用条件确定周期进而求解
知识点
扫码查看完整答案与解析