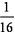- n次独立重复试验中恰好发生k次的概率
- 共66题
近年来,某企业每年消耗电费约24万元,为了节能减排,决定安装一个可使用15年的太阳能供电设备接入本企业电网,安装这种供电设备的工本费(单位:万元)与太阳能电池板的面积(单位:平方米)成正比,比例系数约为0.5,为了保证正常用电,安装后采用太阳能和电能互补供电的模式,假设在此模式下,安装后该企业每年消耗的电费C(单位:万元)与安装的这种太阳能电池板的面积x(单位:平方米)之间的函数关系是C(x)=
(1)试解释C(0)的实际意义,并建立F关于x的函数关系式;
(2)当x为多少平方米时,F取得最小值?最小值是多少万元?
正确答案
见解析
解析
(1)C(0)的实际意义是安装这种太阳能电池板的面积为0时的用电费用,
即未安装电阳能供电设备时全村每年消耗的电费
由C(0)=
所以F=15×

(2)因为

当且仅当
所以当x为55平方米时,F取得最小值为57.5万元
知识点
前不久,省社科院发布了2013年度“城市居民幸福排行榜”,某市成为本年度城市最“幸福城”。随后,某校学生会组织部分同学,用“10分制”随机调查“阳光”社区人们的幸福度.现从调查人群中随机抽取16名,如图所示的茎叶图记录了他们的幸福度分数(以小数点前的一位数字为茎,小数点后的一位数字为叶):
(1)指出这组数据的众数和中位数;
(2)若幸福度不低于9.5分,则称该人的幸福度为“极幸福”。求从这16人中随机选取3人,至多有1人是“极幸福”的概率;
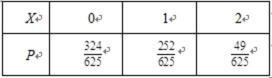
(3)以这16人的样本数据来估计整个社区的总体数据,若从该社区(人数很多)任选3人,记

正确答案
见解析
解析
(1)众数:8.6; 中位数:8.75 ;……………………………2分
(2)设



(3)




所以

另解:


所以

知识点
从0到9这10个数字中任取3个数字组成一个没有重复数字的三位数,则这个数能被 3整除的概率为 ( )
正确答案
解析
0到9这10个数字中,任取3个数字组成一个没有重复数字的三位数,
所有的三位数的个数为
将10个数字分成三组,即被3除余1的有{1,4,7}、被3除余2的有{2,5,8},被3整除的有{3,6,9,0}。
若要求所得的三位数被3整除,则可以分类讨论:
①三个数字均取第一组,或均取第二组,有2 
②若三个数字均取自第三组,则要考虑取出的数字中有无数字0,共有
③若三组各取一个数字,第三组中不取0,有
④若三组各取一个数字,第三组中取0,有
故这个三位数能被3整除的概率是
知识点
一个盒子中装有4张卡片,每张卡片上写有1个数字,数字分别是1、2、3、4,现从盒子中随机抽取卡片。
(1)若一次从中随机抽取3张卡片,求3张卡片上数字之和大于或等于7的概率;
(2)若第一次随机抽取1张卡片,放回后再随机抽取1张卡片,求两次抽取的卡片中至少一次抽到数字2的概率。
正确答案
(1)
解析
(1)设A表示事件“抽取3张卡片上的数字之和大于或等于7”,任取三张卡片,三张卡片上的数字全部可能的结果是(1、2、3),(1、2、4),(1、3、4),(2、3、4),共4种 ……2分
其中数字之和大于或等于7的是(1、2、4),(1、3、4),(2、3、4),共3种…………4分
所以P(A)= 
(2)设
事件B包含的结果有(1、2)(2、1)(2、2)(2、3)(2、4)(3、2)(4、2),
共7个………………………………………………………………10分
所以所求事件的概率为P(B)= 
知识点
已知某人连续5次投掷飞镖的环数分别是8,9,10,10,8,则该组数据的方差s2 =。
正确答案
0.8
解析
8,9,10,10,8的平均分为9
∴该组数据的方差s2=

知识点
甲乙两人进行乒乓球比赛,约定每局胜者得1分,负看得0分,比赛进行到有一人比对方多2分或打满6局时停止,设甲在每局中获胜的概率为


(1)列出随机变量
(2)求

正确答案
见解析
解析
解法1:(1)依题意知,ξ的所有可能值为2,4,6.
设每两局比赛为一轮,则该轮结束时比赛停止的概率为(


若该轮结束时比赛还将继续,则甲、乙在该轮中必是各得一分,此时,该轮比赛结果对下轮比赛是否停止没有影响.从在则有

∴ξ的分布列为

(2)Eξ=2×



解法2:(1)依题意知,ξ的所有可能值为2,4,6.
令Ak表示甲在第k局比赛中获胜,则
由独立性与互斥性得








=2[(









=4(


∴ξ的分布列为

(2)Eξ=2×



知识点
某市为了解今年高中毕业生的体能状况,从本市某校高中毕业班中抽取一个班进行铅球测试,成绩在8.0米(精确到0.1米)以上的为合格. 把所得数据进行整理后,分成6组画出频率分布直方图的一部分(如图),已知从左到右前5个小组的频率分别为0.04,0.10,0.14,0.28,0.30 ,第6小组的频数是7 。
(1)求这次铅球测试成绩合格的人数;
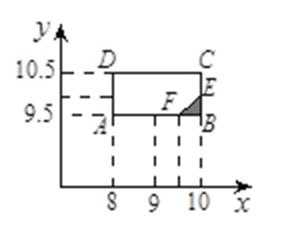
(2)用此次测试结果估计全市毕业生的情况. 若从今年的高中毕业生中随机抽取两名,记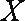
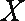
(3)经过多次测试后,甲成绩在8~10米之间,乙成绩在9.5~10.5米之间,现甲、乙各投掷一次,求甲比乙投掷远的概率.
正确答案
(1)36(人)(2)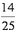
解析
解析:(1)第6小组的频率为1-(0.04+0.10+0.14+0.28+0.30)=0.14,
∴此次测试总人数为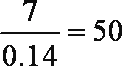
∴第4、5、6组成绩均合格,人数为(0.28+0.30+0.14)×50=36(人) .……………4分
(2)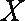
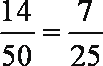
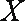
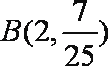
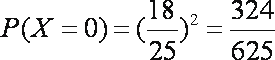
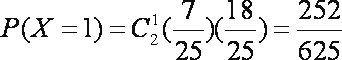
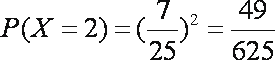
所求分布列为
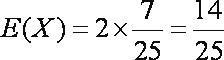
(3)设甲、乙各投掷一次的成绩分别为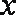
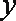
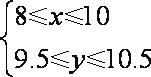
事件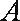

∴由几何概型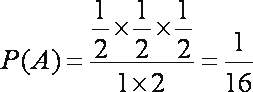
则甲比乙投掷远的概率是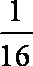
知识点
新交通法规规定:科目三考试分两个项目,在道路驾驶技能考试合格后,还要参加安全文明驾驶常识理论考试,两项都合格后才能获得驾照 。甲乙丙三人道路驾驶技能考试合


(1)求三人中只有一人通过道路驾驶技能考试的概率;
(2)用

正确答案
见解析
解析
解答:(1)
(2)甲获得驾照的概率:

丙获得驾照的概率:


知识点
18.某种产品的质量以其质量指标值衡量,质量指标值越大表明质量越好,且质量指标值大于或等于102的产品为优质品,现用两种新配方(分别称为A配方和B配方)做试验,各生产了100件这种产品,并测量了每件产品的质量指标值,得到下面试验结果:
A配方的频数分布表
B配方的频数分布表
(1)分别估计用A配方,B配方生产的产品的优质品率;
(2)已知用B配方生成的一件产品的利润y(单位:元)与其质量指标值t的关系式为y=
从用B配方生产的产品中任取一件,其利润记为X(单位:元),求X的分布列及数学期望.(以试验结果中质量指标值落入各组的频率作为一件产品的质量指标值落入相应组的概率)
正确答案
见解析。
解析
(1)由试验结果知,用A配方生产的产品中优质的频率为
∴用A配方生产的产品的优质品率的估计值为0.3.
由试验结果知,用B配方生产的产品中优质品的频率为
∴用B配方生产的产品的优质品率的估计值为0.42;
(2)用B配方生产的100件产品中,其质量指标值落入区间
[90,94),[94,102),[102,110]的频率分别为0.04,0.54,0.42,
∴P(X=﹣2)=0.04,P(X=2)=0.54,P(X=4)=0.42,
即X的分布列为
∴X的数学期望值EX=﹣2×0.04+2×0.54+4×0.42=2.68
知识点
20.已知函数f(x)=
(1)求实数a的取值范围;
(2)是否存在实数a,使得函数
(3)设a=

正确答案
解析
解析已在路上飞奔,马上就到!
知识点
扫码查看完整答案与解析