- 列举法计算基本事件数及事件发生的概率
- 共12题
袋中有8个大小相同的小球,其中1个黑球,3个白球,4个红球。
(1)若从袋中一次摸出2个小球,求恰为异色球的概率;
(2)若从袋中一次摸出3个小球,且3个球中,黑球与白球的个数都没有超过红球的个数,记此时红球的个数为


正确答案
见解析。
解析
(1)摸出的2个小球为异色球的种数为
从8个球中摸出2个小球的种数为
故所求概率为
(2)符合条件的摸法包括以下三种:
一种是有1个红球,1个黑球,1个白球,
共有
一种是有2个红球,1个其它颜色球,
共有
一种是所摸得的3小球均为红球,共有
故符合条件的不同摸法共有
由题意知,随机变量





知识点
因台风灾害,我省某水果基地龙眼树严重受损,为此有关专家提出两种拯救龙眼树的方案,每种方案都需分四年实施,若实施方案1,预计第三年可以使龙眼产量恢复到灾前的1.0倍、0.9倍、0.8倍的概率分别是0.3、0.3、0.4;第四年可以使龙眼产量为第三年产量的1.25倍、1.0倍的概率分别是0.5、0.5.若实施方案2,预计第三年可以使龙眼产量达到灾前的1.2倍、1.0倍、0.8倍的概率分别是0.2、0.3、0.5;第四年可以使龙眼产量为第三年产量的1.2倍、1.0倍的概率分别是0.4、0.6.实施每种方案第三年与第四年相互独立,令

(1)写出ξ1、ξ2的分布列;
(2)实施哪种方案,第四年龙眼产量超过灾前产量的概率更大?
(3)不管哪种方案,如果实施后第四年龙眼产量达不到、恰好达到、超过灾前产量,预计利润分别为10万元、15万元、20万元,问实施哪种方案的平均利润更大?
正确答案
见解析。
解析
(1)
(2)由(1)可得ξ1>1的概率P(ξ1>1)= 0.15 + 0.15 = 0.3,
ξ2>1的概率P(ξ2>1)= 0.24 + 0.08 = 0.32,
∵P(ξ2>1)>P(ξ1>1),∴实施方案2,第四年产量超过灾前概率更大.
(3)设实施方案1、2的平均利润分别为利润A、利润B,根据题意,
利润A =(0.2 +0.15)×10 + 0.35×15 +(0.15 + 0.15)×20 = 14.75(万元)
利润B =(0.3 + 0.2)×10 + 0.18×15 + (0.24 + 0.08)×20 = 14.1(万元)
∵利润A>利润B,∴实施方案1平均利润更大。
知识点
某地区组织汉字听写比赛,共有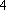

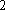

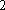




正确答案
17
解析
略
知识点
甲,乙,丙三位学生独立地解同一道题,甲做对的概率为





(1) 求

(2) 记事件



(3)令

正确答案
见解析。
解析
设事件



(1) 由题意知

整理得:

由


(2)由题意知








(3)

∴
故
………………………………………………12分
知识点
如图,从A1(1,0,0),A2(2,0,0),B1(0,1,0),B2(0,2,0),C1(0,0,1),C2(0,0,2)这6个点中随机选取3个点,将这3个点及原点O两两相连构成一个“立体”,记该“立体”的体积为随机变量V(如果选取的3个点与原点在同一个平面内,此时“立体”的体积V=0)。
(1)求V=0的概率;
(2)求V的分布列及数学期望EV.
正确答案
见解析
解析
(1)从6个点中随机选取3个点总共有


(2)V的所有可能取值为0,



由V的分布列可得

知识点
某小组中有6名女同学和4名男同学,从中任意挑选3名同学组成环保志愿者宣传队,则这个宣传队由2名女同学和1名男同学组成的概率是 (结果用分数表示)。
正确答案
解析
略
知识点
对甲、乙、丙、丁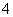
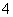

正确答案
18
解析
略
知识点
某超市制定“五一”期间促销方案,当天一次性购物消费额满1000元的顾客可参加“摸球抽奖赢代金券”活动,规则如下:
①每位参与抽奖的顾客从一个装有2个红球和4个白球的箱子中逐次随机摸球,一次只摸出一个球;
②若摸出白球,将其放回箱中,并再次摸球;若摸出红球则不放回,工作人员往箱中补放一白球后,再次摸球;
③如果连续两次摸出白球或两个红球全被摸出,则停止摸球。
停止摸球后根据摸出的红球个数领取代金券,代金券数额Y与摸出的红球个数x满足如下关系:Y=144+72x(单位:元)。
(1)求一位参与抽奖顾客恰好摸球三次即停止摸球的概率;
(2)求随机变量Y的分布列与期望。
正确答案
见解析。
解析
知识点
已知样本7,8,9,x,y的平均数是8,且xy=60,则此样本的标准差是 。
正确答案
解析
解:∵平均数是8,
∴(7+8+9+x+y)÷5=8 ①
xy=60 ②
由两式可得:x=6,y=10,或x=10,y=6。
则此样本的标准差ρ=

知识点
第22届索契冬奥会期间,来自俄罗斯国际奥林匹克大学的男、女大学生共9名志愿者被随机地平均分配到速滑、冰壶、自由式滑雪这三个岗位服务,且速滑岗位至少有一名女大学生志愿者的概率是
(1)求冰壶岗位至少有男、女大学生志愿者各一人的概率;
(2)设

正确答案
见解析
解析
(1)记至少一名女大学生志愿者被分到速滑岗位为事件

“没有女大学生志愿者被分到速滑岗位”,设有女大学生

那么
即女大学生志愿者有3人,男大学生志愿者有6人 ……………………3分
记冰壶岗位至少有男、女大学生志愿者各一人为事件
则
(2)



∴
∴
知识点
扫码查看完整答案与解析






















