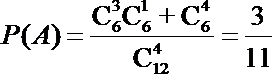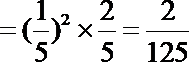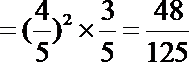- n次独立重复试验中恰好发生k次的概率
- 共66题
19.英语老师要求学生从星期一到星期四每天学习3个英语单词;每周五对一周内所学单词随机抽取若干个进行检测(一周所学的单词每个被抽到的可能性相同)
(1)英语老师随机抽了4个单词进行检测,求至少有3个是后两天学习过的单词的概率;
(2)某学生对后两天所学过的单词每个能默写对的概率为

正确答案
(1)设英语老师抽到的4个单词中,至少含有3个后两天学过的事件为A,则由题意可得
(2)由题意可得ξ可取0,1,2,3,则有P(ξ=0)
P(ξ=1)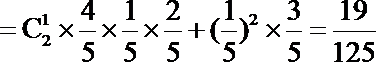
P(ξ=2) 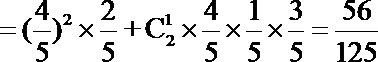
P(ξ=3)
所以ξ的分布列为:
故Eξ=0×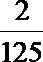
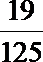
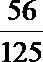
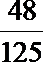
解析
解析已在路上飞奔,马上就到!
知识点
15.某地区为某类人员免费提供财会和计算机培训,参加培训者可以选择参加一项培训、参加两项培训或不参加培训,已知参加过财会培训的有





正确答案
2.7
解析
解析已在路上飞奔,马上就到!
知识点
21.已知某校5个学生的数学和物理成绩如下表
(1)假设在对这


(2)通过大量事实证明发现,一个学生的数学成绩和物理成绩具有很强的线性相关关系的,在上述表格是正确的前提下,用



(3)利用残差分析回归方程的拟合效果,若残差和在
参考数据和公式:



残差和公式为:
正确答案
(1)记事件
(2)


回归直线方程为
(3)
所以为”优拟方程”
解析
解析已在路上飞奔,马上就到!
知识点
18. 某同学参加3门课程的考试.假设该同学第一门课程取得优秀成绩的概率为


(1)求该生至少有1门课程取得优秀成绩的概率;
(2)求

(3)求数学期望
正确答案
事件





(1)由于事件“该生至少有1门课程取得优秀成绩”与事件“


答: 该生至少有1门课程取得优秀成绩的概率是
(2)由题意知
整理得 
由



解析
解析已在路上飞奔,马上就到!
知识点
19.甲、乙两位篮球运动员进行定点投蓝,每人各投4个球,甲投篮命中的概率为

(1)求甲至多命中2个且乙至少命中2个的概率;
(2) 求甲比乙投中的球恰好多两个的概率。
正确答案
(1)设“甲至多命中2个球”为事件A,
“乙至少命中两个球”为事件B,
由题意得,
∴甲至多命中2个球且乙至少命中2个球的概率为
(2)设甲比乙投中的球恰好多两个为事件C
则
P(C)=
解析
解析已在路上飞奔,马上就到!
知识点
扫码查看完整答案与解析