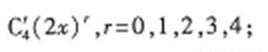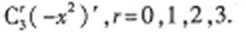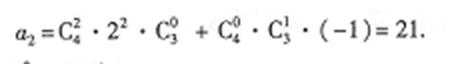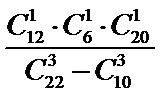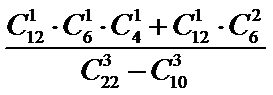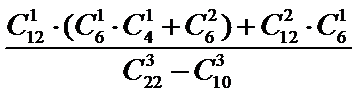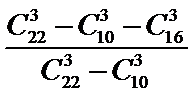- n次独立重复试验中恰好发生k次的概率
- 共66题
“计数原理与概率”模块(10分)
28.已知(1+2x)4(1-x2)3=a0+a1x+a2x2+…a10x10,求a2的值
29.设袋中共有8个球,其中3个白球、5个红球,从袋中随机取出3个球,求至少有1个白球的概率
正确答案
因为( 1+2x)4二项展开式的通项为
( 1一x2 )3二项展开式的通项为
所以
正确答案
从袋中取出3个球,总的取法有 C83=56种;
其中都是红球的取法有 C53 = 10种.
因此,从袋中取出3个球至少有1个白球的概率是
18.某险种的基本保费为a(单位:元),继续购买该险种的投保人称为续保人,续保人本年度的保费与其上年度出险次数的关联如下:
随机调查了该险种的200名续保人在一年内的出险情况,得到如下统计表:
(I)记A为事件:“一续保人本年度的保费不高于基本保费”。求P(A)的估计值;
(II)记B为事件:“一续保人本年度的保费高于基本保费但不高于基本保费的160%”.
求P(B)的估计值;
(III)求续保人本年度平均保费估计值.
正确答案
(Ⅰ)由

解析
(Ⅰ)事件A发生当且仅当一年内出险次数小于2.由所给数据知,一年内险次数小于2的频率为
故P(A)的估计值为0.55.
(Ⅱ)事件B发生当且仅当一年内出险次数大于1且小于4.由是给数据知,学.科网一年内出险次数大于1且小于4的频率为
故P(B)的估计值为0.3.
(Ⅲ)由题所求分布列为:
调查200名续保人的平均保费为
,
因此,续保人本年度平均保费估计值为1.1925a.
保费
考查方向
样本的频率,用频率估计概率,平均值的计算.
解题思路
(I)由数据可知,一年内出险次数小于2次的满足题意,有两种情况,由频数除以总数可以得到P(A)(II) 由数据可知,一年内出险次数大于1次小于4次的满足题意,有两种情况,由频数除以总数可以得到P(B) (III)根据数据,由平均数的计算公式求解结论。
易错点
提议理解不准确,平均值计算的不准确。
4.投篮测试中,每人投3次,至少投中2次才能通过测试。已知某同学每次投篮投中的概率为0.6,且各次投篮是否投中相互独立,则该同学通过测试的概率为( )
正确答案
解析
根据独立重复试验公式得,该同学通过测试的概率为
考查方向
解题思路
本题首先读懂题意,明白通过测试有两种情况,一是三次命中两次,零一种是三次全部命中,根据独立重复试验公式即可得结果。
易错点
本题主要考查独立重复试验的概率公式与互斥事件和概率公式,分类时易错.
知识点
10.某高中数学老师从一张测试卷的12道选择题、4道填空题、6道解答题中任取3道题作分析,则在取到选择题时解答题也取到的概率为( )
正确答案
解析
从12道选择题、4道填空题、6道解答题中任取3道题取到选择题才取法有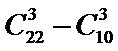
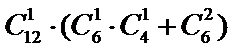
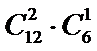
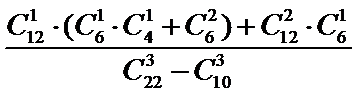
考查方向
解题思路
1.先求任选3道题,取到选择题的解法有多少种;
2.然后求任选的3道题中既有选择题又有解答题的选法有多少种,最后带到古典概型的概率公式中即可。
易错点
1.分类不全,分类没有明确的标准,分类重复等;
2.对于各类情况的算法出错。
知识点
16.已知某种动物服用某种药物一次后当天出现A症状的概率为
(Ⅰ)如果出现A症状即停止试验”,求试验至多持续一个用药周期的概率;
(Ⅱ)如果在一个用药周期内出现3次或4次A症状,则这个用药周期结束后终止试验,试验至多持续两个周期. 设药物试验持续的用药周期数为

正确答案
(Ⅰ)
(Ⅱ)
解析
(Ⅰ)设持续


所以
则
法二:设用药持续最多一个周期为事件

所以
所以
(Ⅱ)随机变量

所以

所以
考查方向
本题主要考察了概率统计,期望的问题,属于中档题,是高考的热点,解决此类题的关键:会用公式算概率和期望。
易错点
1、本题易在读题时因读不懂题意,导致概率无法计算。
2、因期望中随机变量对应的概率算错而导致出错。
知识点
18.某单位考勤制度为早中晚刷脸3次,在规定时间内刷脸3次标记为绿色,刷脸2次标记为蓝色,刷脸1次标记为橙色,刷脸0次标记为红色,若标记为橙色,蓝色,红色需要填写申辩说明理由,现有前一天的考勤记录报表显示为甲办公室共计4人,其中标记红色1人,绿色2人,蓝色1人.乙办公室共计3人,其中标记橙色1人,绿色2人.现从甲乙两个办公室各任意抽取2人.
(1)求抽取的4人标记均为绿色的概率;
(2)若标记为红色,蓝色,橙色的人需要提交申辩,设所抽取的4人需要填写申辩的人数为

正确答案
(1)
(2)分布列为
期望为
解析
本题属于古典概型的常见题型,题目的难度是比较稳定,属于中档偏易题,
(1)直接计算出基本事件总数及符合所求的基本事件数;
(2)分析
(3)列出分布列,求出期望。
(1)设“抽取的4人标记均为绿色”为事件

(2) 





易错点
审题不清和考虑不全面导致出错。
知识点
扫码查看完整答案与解析