- 解三角形
- 共644题
19.在一个特定时段内,以点E为中心的7海里以内海域被设为警戒水域,点E正北55海里处有一个雷达观测站A.某时刻测得一艘匀速直线行驶的船位于点A北偏东45º且与点A相距40




(1)求该船的行驶速度(单位:海里/小时)
(2)若该船不改变航行方向继续行驶,判断它是否会进入警戒水域,并说明理由.
正确答案
解析
解析已在路上飞奔,马上就到!
知识点
10.直角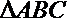
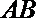
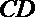
正确答案
解析
解析已在路上飞奔,马上就到!
知识点
16.已知ΔABC为等边三角形,点M在ΔABC外,且MB = 2MC = 2,则MA的最大值是__________。
正确答案
3
解析
试题分析:如图,以M为坐标原点,建立坐标系,则B(2,0),设

又因为

由


考查方向
解题思路
建立坐标系,利用正余弦定理即可求MA的最大值。
易错点
不知如何建立坐标系,对已知条件不知如何应用导致本题无思路。
知识点
已知函数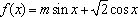
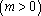
(1)求函数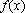
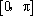
(2)已知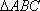
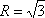
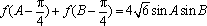
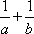
正确答案
(1)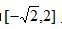
解析
(1)由题意,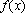
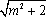
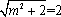
而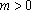
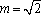
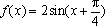
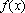
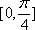
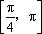
所以函数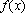
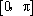
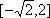
(2)化简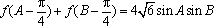
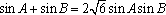
由正弦定理,得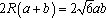
因为△ABC的外接圆半径为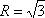
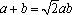
所以
知识点
在





正确答案
60°
解析
解法1:由已知AD=2,∠ADE=60°,得DE=1,AE=
因为





又EC=

因此
解法2:由已知AD=2,∠ADE=60°,得DE=1,AE=
因为




所以




根据余弦定理得
因此
知识点
设





(1)求实数

(2)
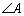




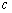



正确答案
见解析。
解析
(1)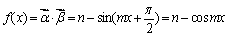
因为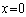
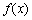
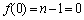
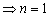
易知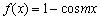

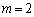

(2)由(Ⅰ)可知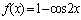
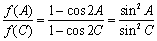
由正弦定理及余弦定理有: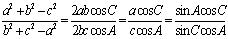
故
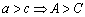
于是
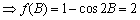
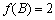
知识点
19. 在△ABC中,角A,B,C的对边分别为a,b,c,且满足(a-c) 
(1)求角B的大小;
(2)若|

正确答案
解析
解析已在路上飞奔,马上就到!
知识点
正确答案
知识点
21.如图,在一条景观道的一端有一个半径为







(1)同学甲打算独自乘坐摩天轮,但是其母亲不放心,于是约定在登上摩天轮座舱



(2)在同学甲向其母亲挥手致意的同时,同一座舱的另一名乘客乙在拍摄地面上的一条绿化带



正确答案
(1)
(2)94米.
解析
(1)

∴

过点


则

∴
∴
答:望远镜的仰角
(2)在

∴
∴

∴
答:绿化带的长度为94米.
考查方向
本题主要考查利用正弦定理解三角形,是一道有实际问题背景的应用题.应用题的考查在近几年的各省高考题中出现的频率非常高,通常与函数、不等式、三角、数列、解析几何、立体几何、向量、概率统计等知识点相结合进行命题,是高考的热点问题.
解题思路
题(1),摩天轮做匀速转动,逆时针15分钟转一圈,可得5分钟转过120°,过点C作CH⊥AB于点H,解三角形可得望远镜的仰角
(2)由题意可求CD,利用正弦定理即可解得BD的长度.
易错点
面对题设条件,无法确定什么时候用正弦定理什么时候用余弦定理或其它相关知识求解三角形的边与角.
知识点
16.已知函数


(I)求
(II)在




正确答案
解:(Ⅰ)因为

所以

解
得:
所以函数
(Ⅱ) 因为
得
因为

所以

所以
根据正弦函数的图象可以看出,

此时

所以
解析
见答案
考查方向
本题主要考查正弦定理和余弦定理的性质,属于基础题
解题思路
根据题意换成三角函数一般形式,然后根据函数最值判断,第二问求出ABC角度的大小进而判定三角形形状。
易错点
混淆两个定理的性质
知识点
扫码查看完整答案与解析