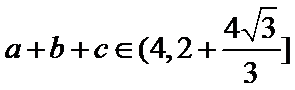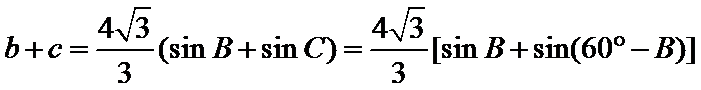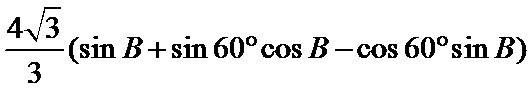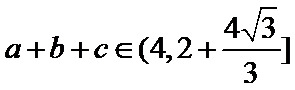- 解三角形
- 共644题
在




16.求
17.若


正确答案
解析
解: 




考查方向
解题思路
先通过共线,列出方程,然后用正弦定理,将边转成角,用利用和角公式,先用余弦定量得到a的方程,为求BD的模,可以通过平方再开方的办法间接的模。
易错点
对向量共线掌握不准,对三角恒等变换及正余定理的应用不熟练
正确答案
解析
解: 

解得

将


考查方向
解题思路
先通过共线,列出方程,然后用正弦定理,将边转成角,用利用和角公式,先用余弦定量得到a的方程,为求BD的模,可以通过平方再开方的办法间接的模。
易错点
对向量共线掌握不准,对三角恒等变换及正余定理的应用不熟练
12.已知A、B、C为△ABC的三个内角,向量m满足|m|=







正确答案
解析
如图假设AB=2,BC=
∴P的轨迹为椭圆且
考查方向
解题思路
1)由向量向量m的模长得出
2)动点P使得|



3)由|
4)根据一元二次函数的性质得出结果
易错点
主要易错于几何意义的构建
知识点
在△ABC中,角A,B,C的对边分别为a,b,c,向量

16.求角
17.若a=6,求△ABC面积的最大值.
正确答案
(Ⅰ)
解析
试题分析:本题属于三角函数的基本问题,题目的难度是逐渐由易到难,(1)直接按步骤来求解,(2)要注意注明基本不等式等号成立的条件.
(Ⅰ)因为向量

所以
由正弦定理得
即
由于B是三角形的内角,
则

考查方向
解题思路
本题考查平面向量共线的坐标表示、解三角形,解题步骤如下:
1)利用平面向量共线的坐标表示得到三角形的边角关系;
2)利用正弦定理将边角关系转化为角角关系,利用三角形的内角和定理进行求解;
3)利用余弦定理得到边边关系;
4)利用基本不等式和三角形的面积公式进行求解。
易错点
1)易混淆平面向量共线的坐标表示与垂直的坐标表示;
2)利用基本不等式求最值时,忽视注明等号成立的条件.
正确答案
(Ⅱ)
解析
试题分析:本题属于三角函数的基本问题,题目的难度是逐渐由易到难,(1)直接按步骤来求解,(2)要注意注明基本不等式等号成立的条件.
(Ⅱ)因为
所以
且仅当b=c时取得等号,所以
故
所以当b=c时,

考查方向
解题思路
本题考查平面向量共线的坐标表示、解三角形,解题步骤如下:
1)利用平面向量共线的坐标表示得到三角形的边角关系;
2)利用正弦定理将边角关系转化为角角关系,利用三角形的内角和定理进行求解;
3)利用余弦定理得到边边关系;
4)利用基本不等式和三角形的面积公式进行求解。
易错点
1)易混淆平面向量共线的坐标表示与垂直的坐标表示;
2)利用基本不等式求最值时,忽视注明等号成立的条件.
已知△ABC中,内角A,B,C的对边分别为a,b,c,且2cos2=sin B,b=1.
15.若A=,求边c;
16.若a=2c,求△ABC的面积.
正确答案
解析
解:由已知可得1+cos B=sin B…………2分
∴sin=.…………3分 又0
∴c=·sin C=.…………6分
考查方向
解题思路
先用二倍角公式降幂升角,然后再应用辅助角公式,求得角B、角C, 再由正弦定理解出c边长
易错点
三角恒等变换公式选择不准确,正余定理应用不熟练
正确答案
.
解析
解:由15题知B=,…………7分∴由余弦定理得b2=a2+c2-2accos B.……8分
又a=2c,∴c2=,…………10分∴△ABC的面积S=acsin B=.…………12分
考查方向
解题思路
根据第一问的角B的值, 得到a,c方程,又由a=2c,解出c,用 acsin B求面积。
易错点
三角恒等变换公式选择不准确,正余定理应用不熟练
13.在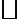
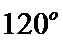
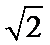
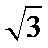
正确答案
解析
由正弦定理得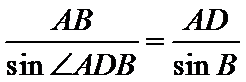
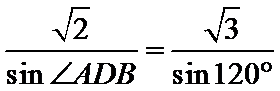
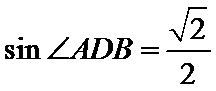

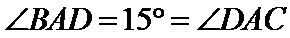
所以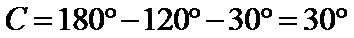
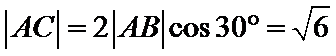
考查方向
解题思路
解三角形就是根据正弦定理和余弦定理得出方程进行的.当已知三角形边长的比时使用正弦定理可以转化为边的对角的正弦的比值,本例第一题就是在这种思想指导下求解的;当已知三角形三边之间的关系式,特别是边的二次关系式时要考虑根据余弦定理把边的关系转化为角的余弦关系式,再考虑问题的下一步解决方法.
易错点
边角关系的转化
知识点
在△ABC中,角A、B、C所对的边分别为a、b、c,且满足cos2C-cos2A=2sin(

17.求角A的值;
18.若a=
正确答案
见解析
解析
(1)由已知得
化简得


考查方向
解题思路
该题解题思路如下
1)利用倍角公式
2)利用特殊角的三角函数求值得到角A,
3)使用正弦定理,进行边角之间的转换
4)根据角的取值范围得到答案
易错点
该题易于忽略了对A的范围的判断,该题属于中档题
正确答案
见解析
解析
解:
(2)由正弦定理

故
因为


所以
考查方向
解题思路
该题解题思路如下
1)利用倍角公式
2)利用特殊角的三角函数求值得到角A,
3)使用正弦定理,进行边角之间的转换
4)根据角的取值范围得到答案
易错点
该题易于忽略了对A的范围的判断,该题属于中档题
在




正确答案
1
解析
解题思路
已知条件中给的是边,要想用上这些已知条件,必须把所求的角化成边,而正弦定理、余弦定理是实现的途径。
易错点
把正弦定理化角为边的作用错误放大,如:
教师点评
本题属于解三角形的题目,这一章无非涉及到四个知识点:正弦定理、余弦定理、三角形面积公式、实际应用。复习时要注意掌握各自内容、灵活应用,以及熟练正余弦相结合的综合应用的题目。
知识点
在



17.求
18.若




正确答案
(1)
解析
试题分析:本题属于解三角形问题,属于基础题,主要考查两个定理的应用以及三角形的面积公式。具体解答步骤如下:
(Ⅰ)由正弦定理,
可得
所以
所以
因为


考查方向
解题思路
本题考查解三解形,解题步骤如下:
1)利用正弦定理及三角恒等变换求出C。
2)通过面积公式及
3)根据a,b的两组解分别求

易错点
1、利用余弦定理增加运算量; 2、第二问解三角形时遗漏一组解。
正确答案
(2)

解析
试题分析:本题属于解三角形问题,属于基础题,主要考查两个定理的应用以及三角形的面积公式。具体解答步骤如下:
(Ⅱ)解法一:由已知
所以


当

所以
所以


因为

在

当
所以

(Ⅱ)解法二:在


因为

由已知

又
解得
考查方向
解题思路
本题考查解三解形,解题步骤如下:
1)利用正弦定理及三角恒等变换求出C。
2)通过面积公式及
3)根据a,b的两组解分别求

易错点
1、利用余弦定理增加运算量; 2、第二问解三角形时遗漏一组解。
在




正确答案
1
解析
解题思路
已知条件中给的是边,要想用上这些已知条件,必须把所求的角化成边,而正弦定理、余弦定理是实现的途径。
易错点
把正弦定理化角为边的作用错误放大,如:
教师点评
本题属于解三角形的题目,这一章无非涉及到四个知识点:正弦定理、余弦定理、三角形面积公式、实际应用。复习时要注意掌握各自内容、灵活应用,以及熟练正余弦相结合的综合应用的题目。
知识点
在△ABC中,已知a,b, c分别是角A,B,C的对边,且满足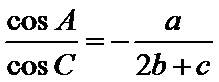
17.求角A的大小;
18.若a=2,求△ABC的周长的取值范围.
正确答案
(1)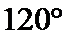
解析
(1)由正弦定理,得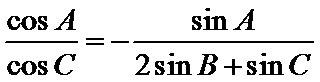
∴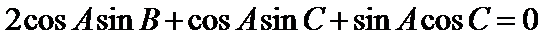
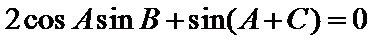
∵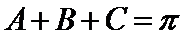
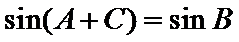
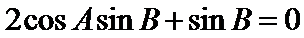
∵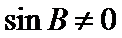
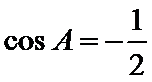
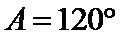
考查方向
解题思路
(1)利用已知条件和正弦定理求出角A(2)利用(1)中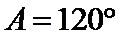
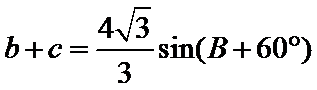
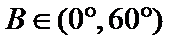
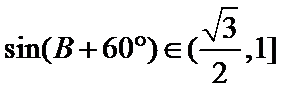
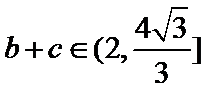
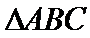
易错点
通过正弦定理表示三边即周长,易忽视角的范围出错。
正确答案
(2)
解析
(2)由正弦定理,得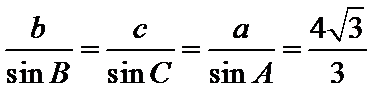
∴
=
=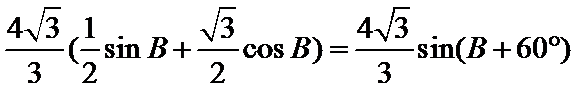
∵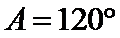
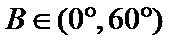
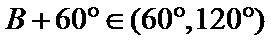
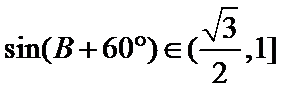
∴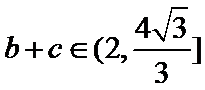
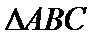
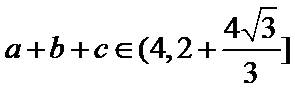
考查方向
解题思路
(1)利用已知条件和正弦定理求出角A(2)利用(1)中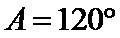
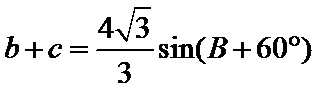
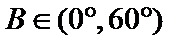
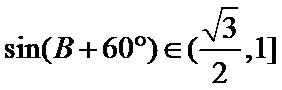
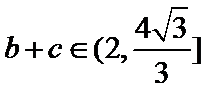
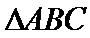
易错点
通过正弦定理表示三边即周长,易忽视角的范围出错。
扫码查看完整答案与解析