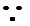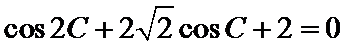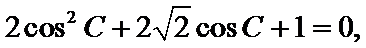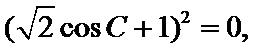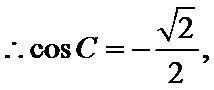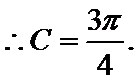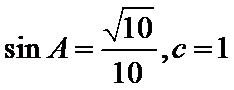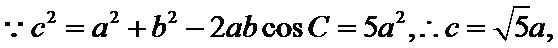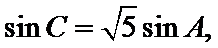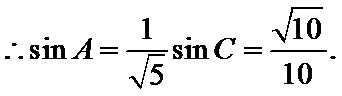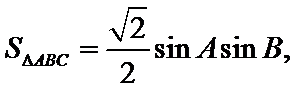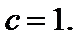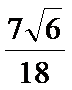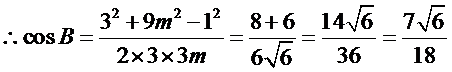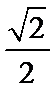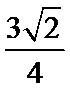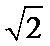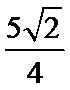- 解三角形
- 共644题
已知



17.求
18.若

正确答案

解析
∵

∴




考查方向
解题思路
第一问中用两角和差公式和三角恒等变换化简得到

易错点
第一问中想不到将角

正确答案

解析
∵




∴


考查方向
解题思路
第二问中用倍余弦定理得到一个角,在用三角形面积公式求得面积。
易错点
第二问中用余弦定理求角时容易将特殊角记错。
(2016上海奉贤一模) 用一4个倍放大镜照△
正确答案
知识点
在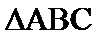
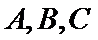
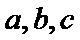
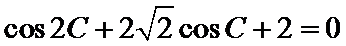
16.求角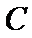
17.若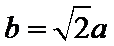
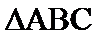

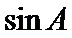

正确答案
(1) 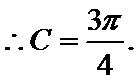
解析
(Ⅰ)
即
又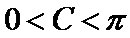
考查方向
解题思路
根据题中给出等式求出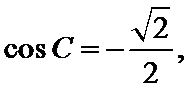
易错点
对于正弦定理的反复转化不明白。
正确答案
(2)
解析
(Ⅱ)
由正弦定理,得
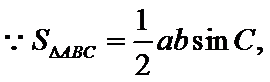
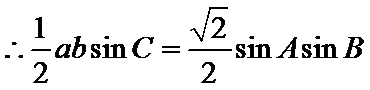
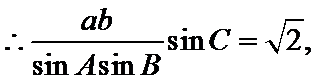
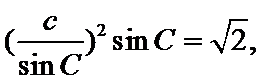
考查方向
解题思路
先根据余弦定理求出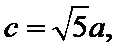
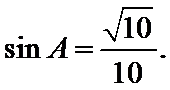
易错点
不知道该如何使用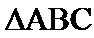
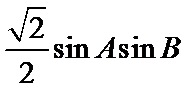
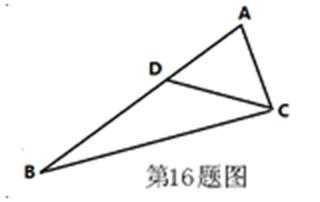
△ABC中,
17.求BC的长;
18.求△DBC的面积。
正确答案
3
解析
解∵cos∠ABC
在△ABC中,设BC=a,AC=3b ∴9b2=
在△ABD中, cos∠ADB=
在△BDC中, cos∠BDC=
cos∠ADB=-cos∠BDC


由①②
考查方向
解题思路
利用角的关系,利用余弦定理得到边的关系,通过解方程求得BC长。
易错点
含有a的方程不易处理。
正确答案
解析
解

考查方向
解题思路
利用角的关系,利用余弦定理得到边的关系,通过解方程求得BC长。
易错点
含有a的方程不易处理。
5. 在




正确答案
解析
由正弦定理得



考查方向
解题思路
1.先利用正弦定理求出角C;2.利用大边对大角求出角C的准确值。
易错点
1.不知道应该用什么定理;2.不会根据大边对大角舍去一个角,导致结果出错。
知识点
如图,在平面四边形





17.求
18.求
正确答案
(1) 
解析
(Ⅰ)在

即


由正
考查方向
解题思路
先利用余弦定理求出
易错点
不知道该在哪个三角形中使用什么定理;
正确答案
;(2)
解析
(Ⅱ)由(Ⅰ)有:

所以
由正弦定理得:
考查方向
解题思路
利用第(1)问的结论求出
易错点
意识不到
如图所示,在四边形





16.求△
17.若

正确答案
见解析
解析
(Ⅰ)
因为

所以△ACD的面积
考查方向
解题思路
利用已知条件求出∠D角的正弦函数值,然后求
易错点
主要易错于计算出错,
正确答案
见解析
解析
(Ⅱ)在△ACD中,
所以
在△ABC中,
把已知条件代入并化简得:

考查方向
解题思路
利用余弦定理求出AC,通过
易错点
主要易错于计算出错,
16.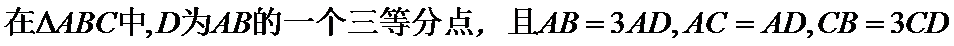
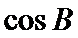
正确答案
解析
令AC=AD=1,CD=x > 0 , 则 AB=3 , BC= 3x ,
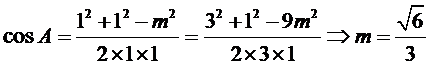
考查方向
解题思路
1.先设出题中需要的线段的长度;
2.根据余弦定理求出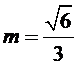
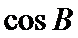
易错点
1.不会设出长度解决问题;
2.不会利用角A的余弦构造方程解方程。
知识点
11.已知函数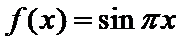
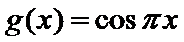
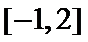
正确答案
解析
由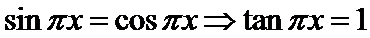
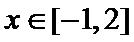
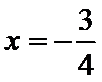
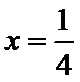
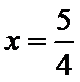
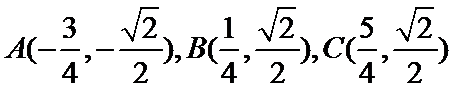
故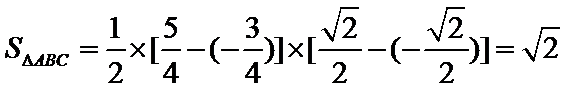
考查方向
解题思路
1.先根据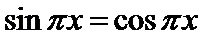
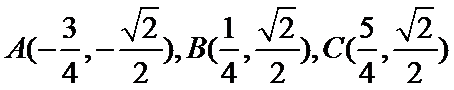
易错点
1.不会结合图像求出A,B,C的坐标;2.不会做函数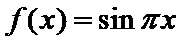
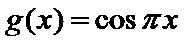
知识点
已知向量

17.若

18.在




正确答案
解析

得
即


考查方向
解题思路
先通过向量垂直,得到三角关系,利用辅助角公式得到三角函数的解析式y=sin(x-



易错点
向量的坐标运算,三角函数的恒等变换
正确答案
(0,
解析
由

∴







考查方向
解题思路
将边用正弦定理进行转化,得到cosA=


易错点
向量的坐标运算,三角函数的恒等变换
扫码查看完整答案与解析