- 解三角形
- 共644题


17.求角B的大小;
18.若BD为AC边上的中线,

正确答案
见解析
解析









考查方向
解题思路
利用正弦定理求角度
易错点
正弦定理、余弦定理的性质掌握不好
正确答案
见解析
解析
法一:在三角形









法二: 延长













考查方向
解题思路
用余弦定理求面积
易错点
正弦定理、余弦定理的性质掌握不好
15. 在

(1)求
(2)若点D在


正确答案
见解析
解析
解:如图, 设




又由正弦定理得
由题设知

在

考查方向
解题思路
(1)用余弦定理求a
(2)由正弦定理求sinB
(3)在
易错点
忽略数形结合思想在本题中的作用。
知识点
13.海轮“和谐号”从A处以每小时21海里的速度出发,海轮“奋斗号”在A处北偏东

正确答案
解析
由题意做出平面图,如图所示,





考查方向
解题思路
1)根据题意,以及方向角,画出平面图形;
2)在
易错点
本题应当根据题意画出准确的图像,学生容易画错,计算也是 比较难的;
知识点
请你谈一谈对“不同生产方式以及生产工艺中,生产物流管理所采用的方法和手段是不同的。”这句话的理解。
正确答案
测试
函数f(x)=sin(x+2φ)-2sin φcos(x+φ)的最大值为________。
正确答案
1
解析
函数f(x)=sin(x+2φ)-2sin φcos(x+φ)=sin[(x+φ)+φ]-2sin φcos(x+φ)=sin(x+φ)cos φ-cos(x+φ)sin φ=sin x,故其最大值为1.
知识点
已知函数
(1)求函数

(2)若

正确答案
见解析。
解析
(1)解:由
所以函数
因为





(2)解:由(1)可知
又因为
由
从而
所以
知识点
函数
正确答案
解析


=

当


知识点
设函数

(1)若


(2)若




正确答案
见解析。
解析
(1)
当

而


此时



∴


(2)依题意


整理,得
又


而





知识点
设





(1)求实数

(2)
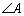




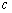



正确答案
见解析。
解析
(1)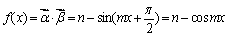
因为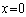
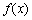
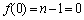
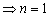
易知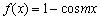

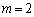

(2)由(Ⅰ)可知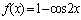
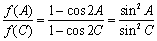
由正弦定理及余弦定理有: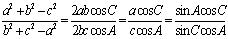
故
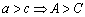
于是
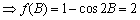
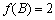
知识点
13.如图,一辆汽车在一条水平的公路上向正西行驶,到





正确答案
解析
解析已在路上飞奔,马上就到!
知识点
扫码查看完整答案与解析





















