- 不等式的性质
- 共451题
1
题型：
单选题
|
对于任意的x∈R，不等式
Aa<2
Ba≤2
Ca≤3
Da<3
正确答案
D
解析
略
知识点
不等式的性质
1
题型：简答题
|
已知函数
（1）当
（2）若关于
正确答案
（1）
解析
（1）当a=2时， f（x）>4即为|x-2|>1
所以x-2<-1或x-2>1 ……………………2分
即x<1或x>3
所以f（x）>4的解集为{x| x<1或x>3} ……………………4分
（2）由题意得
∴
即|x-a|<2-a，
又因为
又
知识点
不等式的性质
1
题型：简答题
|
已知函数
（1）当
（2）若不等式
正确答案
见解析
解析
解析：（1）由
解得：
（2）由不等式的性质得：
要使不等式
解得：
所以实数
知识点
不等式的性质
1
题型：填空题
|
已知
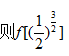
正确答案
解析
由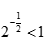
而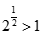
知识点
不等式的性质
1
题型：简答题
|
已知函数
（1）当
（2）若关于
正确答案
（1）
解析
（1）由题意
解得
（2） 
由题意,不等式
而
知识点
不等式的性质
下一知识点 : 不等式的应用
扫码查看完整答案与解析