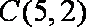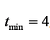- 不等式的性质
- 共451题
已知关于x的不等式

(1)当
(2)若不等式有解,求实数
正确答案
(1)
解析
解析:(1)当a=4时,不等式即|2x+1|-|x-1|≤2,当x<−




综上,不等式的解集为{x|−4≤x≤
(2)设f(x)=|2x+1|-|x-1|=
故f(x)的最小值为−


即a的取值范围是
知识点
如图所示的韦恩图,中







( )
正确答案
解析
依题意,





知识点
如图,五面体





(1)




(2)当


正确答案
见解析
解析
解析:(1)当



证明:连结




∴




∵





(2)建立空间直角坐标系
则




所以

设


令


而平面

所以


知识点
已知函数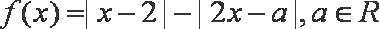
(1)当
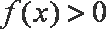
(2)当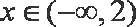
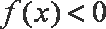
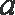
正确答案
见解析
解析
解析:(1)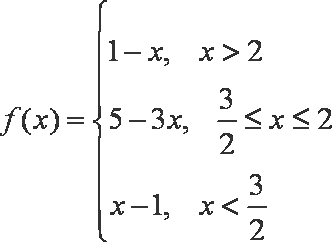
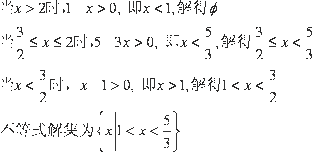
(2)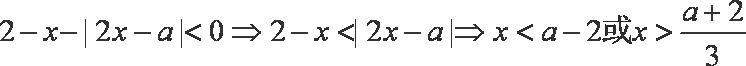
即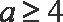
知识点
在平面直角坐标系中,定义点
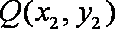
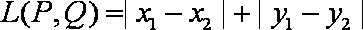
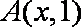
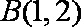
(1)若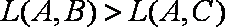
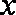
(2)当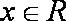
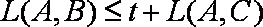

正确答案
(1)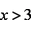
解析
解析:(1)由定义得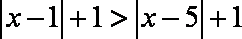
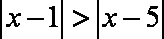
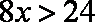
解得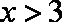
(2)当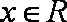
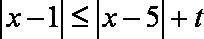
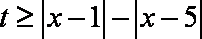
法一:函数 令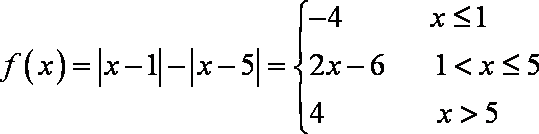
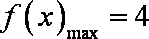
要使原不等式恒成立只要
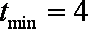
法二:三角不等式性质 因为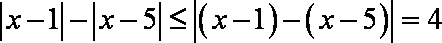
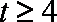
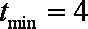
知识点
扫码查看完整答案与解析