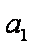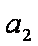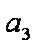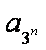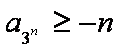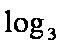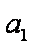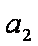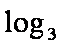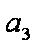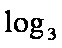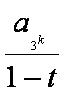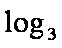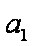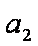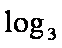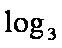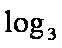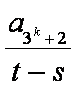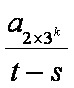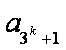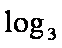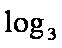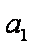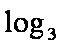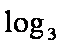- 不等式的性质
- 共451题
岳阳市临港新区自2009年6月8日开港来,吸引了一批投资过亿元的现代工业和物流储运企业落户。根据规划,2025年新港将全部建成13个泊位,从2014年(第一年)开始对其中某个子港口今后10年的发展规划,有如下两种方案:
方案甲:按现状进行运营。据测算,每年可收入800万元,但由于港口淤积日益严重,从明年开始需投资进行清淤,第一年投资50万元,以后逐年递增20万元。
方案乙:从2014年起开始投资4000万元进港口改造,以彻底根治港口淤积并提高吞吐能力。港口改造需用时4年,在此期间边改造边运营.据测算,开始改造后港口第一年的收入为400万元,在以后的4年中,每年收入都比上一年增长50%,而后各年的收入都稳定在第5年的水平上。
(1)至少经过多少年,方案乙能收回投资(累计总收益为正数)?
(2)到哪一年,方案乙的累计总收益超过方案甲?(收益=收入-投资)
正确答案
(1)5
(2)2020
解析
(1)设从2014年开始经过n年,方案乙的累计总收益为正数。
在方案乙中,前4年的总收入为 
故n必定不小于4,则由 
解得 
答: 从2014开始至少经过5年,方案乙能收回投资。
(2)设从2014年开始经过n年方案甲与方案乙的累计总收益分别为y1,y2万元,
则
当n≤4时,则y1>0,y2<0,可得y1>y2.
当n>5时,
令y1<y2,可得
由
答:到2020年,方案乙的累计总收益超过方案甲。
知识点
(1)已知
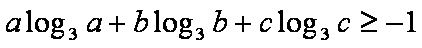
(2)已知

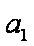

正确答案
见解析。
解析
(1)证明:

那么f ′ (a)= log3a-log3(1-a-b),当a∈(0,


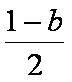


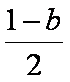

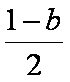
得:g′(b)= log3b-log3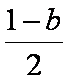
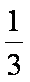






alog3a+blog3b+clog3c≥-1当a=b=c=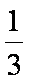
(2)证明:n=1时,
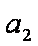

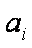
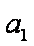
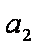

设n=k时结论成立,即





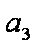

那么,n=k+1时,若




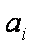
令
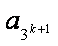







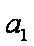
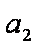
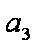

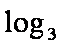
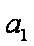




设




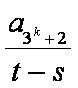

由归纳假设:




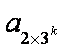
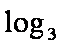


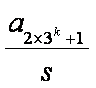






将①②③两边分别相加得:
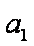
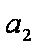

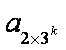
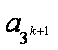


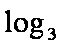
而(1-t)+(t-s)+s=1,(1-t)>0,(t-s) >0,s >0。
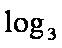



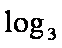

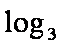




知识点
设



正确答案
-3
解析
画出约束条件
由可行域知:目标函数
取最小值-3.
知识点
若不等式

正确答案
解析
根据几何意义可知:要使不等式



知识点
已知函数
(1)求函数
(2)若关于




(3)某同学发现:总存在正实数



[来源:
正确答案
见解析。
解析
(1)定义域为



当


∴



(2)∵不等式


∴分离



∴下面即求


∵



当



∴
当


∴
当





∴
综上得:
当
当
当

(3)正确 ,

注:理由如下,考虑函数







∴
∴总存在正实数


即


知识点
扫码查看完整答案与解析