- 不等式的性质
- 共451题
11.定义域为R的偶函数f（x）满足∀x∈R，有f（x+2）=f（x）﹣f（1），且当x∈[2，3]时，f（x）=﹣2x2+12x﹣18.若函数y=f（x）﹣loga（x+1）至少有三个零点，则a的取值范围是（ ）
A（0，
B（0，
C（0，
D（0，
正确答案
解析
∵f（x+2）=f（x）﹣f（1），且f（x）是定义域为R的偶函数，
令x=﹣1可得f（﹣1+2）=f（﹣1）﹣f（1），f（﹣1）=f（1），
即 f（1）=0 则有，f（x+2）=f（x），
∴f（x）是周期为2的偶函数。
当x∈[2，3]时，f（x）=﹣2x2+12x﹣18=﹣2（x﹣3）2，
函数的图象为开口向下、顶点为（3，0）的抛物线。
∵函数y=f（x）﹣loga（|x|+1）在（0，+∞）上
至少有三个零点，
令g（x）=loga（|x|+1），则f（x）的图象和g（x）的图象至少有3个交点。
∵f（x）≤0，∴g（x）≤0，可得a＜1。
要使函数y=f（x）﹣loga（|x|+1）在（0，+∞）上至少有三个零点，
则有g（2）＞f（2），可得 loga（2+1）＞f（2）=﹣2，
∴loga3＞﹣2，∴3＜
又a＞0，∴0＜a＜
知识点
9.下列命题中正确的有（ ）
①设有一个回归方程
②命题P：“
③设随机变量X服从正态分布N(0，1)，若P(X>1)=p，则P(-1<X<0)=
④在一个2×2列联表中，由计算得k2=6．679，则有99％的把握确认这两个变量间有关系．
本题可以参考独立性检验临界值表
正确答案
解析
①变量x增加一个单位时，y平均减少3个单位，所以错误。②正确。③
知识点
6.设实数x，y满足不等式组
A[1,2]
B[1,4]
C[
D[2,4]
正确答案
解析
如图所示，不等式组表示的平面区域是△ABC的内部(含边界)，x2＋y2表示的是此区域内的点(x，y)到原点距离的平方.从图中可知最短距离为原点到直线BC的距离，其值为1；最远的距离为AO，其值为2，故x2＋y2的取值范围是[1,4].
知识点
13. 已知
正确答案
解析
略
知识点
14.若实数x，y满足
正确答案
{0}
解析
令
知识点
6.设
A
B
C
D
正确答案
解析
略
知识点
20.已知函数
（1）当
（2）当
正确答案
（1）
（2）
解析
（1）∵
又∵
∴
（2）∵
令
对于
知识点
11.若对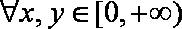
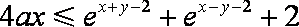
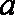
A
B1
C2
D
正确答案
解析
因为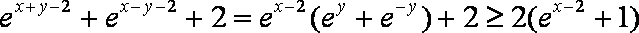
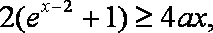
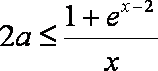
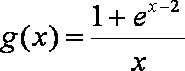
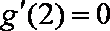
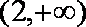
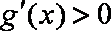
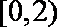
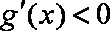
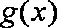
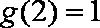
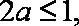
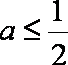
知识点
15.若不等式|2x－1|＋|x＋2|≥a2＋
正确答案
解析
|2x－1|＋|x＋2|＝
知识点
18.（本小题满分13分）已知函数f(x)＝ln x，
（1）若f(x)与g(x)在x＝1处相切，求g(x)的表达式；
（2）若φ(x)＝
正确答案
见解析。
解析
（1）由已知得f′(x)＝
又∵g（1）＝0＝
（2）∵φ(x)＝
∴φ′(x)＝
即x2－(2m－2)x＋1≥0在[1，＋∞)上恒成立，
则2m－2≤x＋
∵x＋
故数m的取值范围是(－∞，2].
知识点
扫码查看完整答案与解析