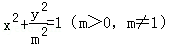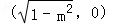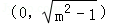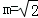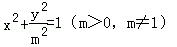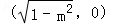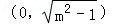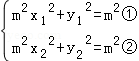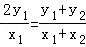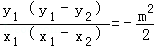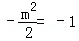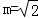- 不等式的应用
- 共30题
请你谈一谈对“不同生产方式以及生产工艺中,生产物流管理所采用的方法和手段是不同的。”这句话的理解。
正确答案
测试
设变量x,y满足约束条件

正确答案
-4
解析
在坐标系中画出可行域,如图所示
由z=3x﹣2y可得y=

平移直线3x﹣2y=0经过点A时,z最小,
由
则目标函数z=3x﹣2y的最小值为﹣4。
故答案为:﹣4。
知识点
已知函数
(1)若

(2)若




正确答案
见解析。
解析
知识点
设A是单位圆x2+y2=1上的任意一点,i是过点A与x轴垂直的直线,D是直线i与x轴的交点,点M在直线l上,且满足丨DM丨=m丨DA丨(m>0,且m≠1),当点A在圆上运动时,记点M的轨迹为曲线C。
(1)求曲线C的方程,判断曲线C为何种圆锥曲线,并求焦点坐标;
(2)过原点且斜率为k的直线交曲线C于P、Q两点,其中P在第一象限,它在y轴上的射影为点N,直线QN交曲线C于另一点H,是否存在m,使得对任意的k>0,都有PQ⊥PH?若存在,求m的值;若不存在,请说明理由。
正确答案
(1)C的方程为
0<m<1时,曲线C是焦点在x轴上的椭圆,两焦点坐标分别为(
m>1时,曲线C是焦点在y轴上的椭圆,两焦点坐标分别为(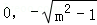
(2)存在,
解析
(1)设M(x,y),A(x0,y0)
∵丨DM丨=m丨DA丨,∴x=x0,|y|=m|y0
∴x0=x,|y0|=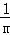
∵点A在圆上运动,∴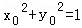
①代入②即得所求曲线C的方程为
∵m∈(0,1)∪(1,+∞),
∴0<m<1时,曲线C是焦点在x轴上的椭圆,两焦点坐标分别为(
m>1时,曲线C是焦点在y轴上的椭圆,两焦点坐标分别为(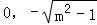
(2)∀x1∈(0,1),设P(x1,y1),H(x2,y2),则Q(x2,y2),N(0,y1),
∵P,H两点在椭圆C上,∴
①﹣②可得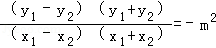
∵Q,N,H三点共线,∴kQN=kQH,∴
∴kPQ•kPH=
∵PQ⊥PH,∴kPQ•kPH=﹣1
∴
∵m>0,∴
故存在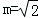
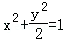
知识点
不等式
正确答案
解析


知识点
阅读下边的程序框图,运行相应的程序,则输出
正确答案
解析
运算过程依次为:
当

当

当

当


知识点
设f(x)是定义在[a,b]上的函数,若存在c
(1)已知
(2)设
①证明:对任意
②记函数

正确答案
见解析。
解析
知识点
方程
正确答案
解析
原方程整理后变为
知识点
已知点

正确答案
解析
∵点A(﹣2,3)在抛物线C:y2=2px的准线上,
即准线方程为:x=﹣2,
∴p>0,
∴抛物线C:y2=8x,在第一象限的方程为y=2
设切点B(m,n),则n=2
又导数y′=2

∴




解得


∴切点B(8,8),又F(2,0),
∴直线BF的斜率为
知识点
已知变量


正确答案
6
解析
先画出可行域(如图),
与原点




知识点
扫码查看完整答案与解析