- 等差数列的判断与证明
- 共87题
请你谈一谈对“不同生产方式以及生产工艺中,生产物流管理所采用的方法和手段是不同的。”这句话的理解。
正确答案
测试
设函数



正确答案
解析
∵
∴
∴
∴
知识点
设数列




(1)求数列
(2)若



正确答案
见解析
解析
由
所以,

而

(2)
知识点
已知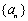

(1)当
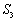
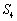
(2)当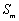
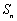
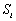
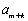
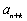
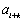
正确答案
见解析
解析
(1)由已知,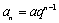
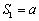
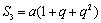

当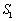
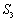
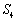
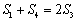
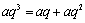
化简得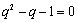
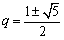
(2)若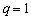
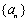
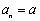
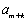
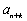
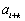
若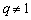
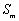
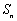
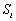
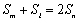
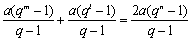
整理得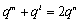
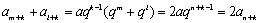
所以,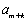
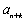
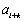
知识点
给定数列a1,a2,…,an,对i=1,2,…,n-1,该数列的前i项的最大值记为Ai,后n-i项ai+1,ai+2,…,an的最小值记为Bi,di=Ai-Bi.
(1)设数列{an}为3,4,7,1,写出d1,d2,d3的值;
(2)设a1,a2,…,an(n≥4)是公比大于1的等比数列,且a1>0.证明:d1,d2,…,dn-1是等比数列;
(3)设d1,d2,…,dn-1是公差大于0的等差数列,且d1>0.证明:a1,a2,…,an-1是等差数列。
正确答案
见解析
解析
(1)d1=2,d2=3,d3=6.
(2)因为a1>0,公比q>1,
所以a1,a2,…,an是递增数列。
因此,对i=1,2,…,n-1,Ai=ai,Bi=ai+1.
于是对i=1,2,…,n-1,
di=Ai-Bi=ai-ai+1=a1(1-q)qi-1.
因此di≠0且
即d1,d2,…,dn-1是等比数列。
(3)设d为d1,d2,…,dn-1的公差。
对1≤i≤n-2,因为Bi≤Bi+1,d>0,
所以Ai+1=Bi+1+di+1≥Bi+di+d>Bi+di=Ai.
又因为Ai+1=max{Ai,ai+1},
所以ai+1=Ai+1>Ai≥ai.
从而a1,a2,…,an-1是递增数列。
因此Ai=ai(i=1,2,…,n-1)。
又因为B1=A1-d1=a1-d1<a1,
所以B1<a1<a2<…<an-1.
因此an=B1.
所以B1=B2=…=Bn-1=an.
所以ai=Ai=Bi+di=an+di.
因此对i=1,2,…,n-2都有ai+1-ai=di+1-di=d,即a1,a2,…,an-1是等差数列。
知识点
扫码查看完整答案与解析














