- 指数与指数函数
- 共570题
电视传媒为了解某市100万观众对足球节目的收视情况,随机抽取了100名观众进行调查,如图是根据调查结果绘制的观众每周平均收看足球节目时间的频率分布直方图,将每周平均收看足球节目时间不低于1.5小时的观众称为“足球迷”, 并将其中每周平均收看足球节目时间不低于2.5小时的观众称为“铁杆足球迷”。
(1)试估算该市“足球迷”的人数,并指出其中“铁杆足球迷”约为多少人;
(2)该市要举办一场足球比赛,已知该市的足球场可容纳10万名观众,根据调查,如果票价定为100元/张,则非“足球迷”均不会到现场观看,而“足球迷”均愿意前往现场观看,如果票价提高



正确答案
(1)3万人(2)140元
解析
(1)样本中“足球迷”出现的频率=

“铁杆足球迷”=
所以16万“足球迷”中,“铁杆足球迷”约有3万人.
(2)设票价为


令
化简得:
解得:

即平均票价至少定为100+40=140元,才能使前往现场观看足球比赛的“足球迷”不超过10万人.
知识点
已知


正确答案
解析
略
知识点
已知函数


(1)求函数
(2)若函数


正确答案
见解析
解析
解析:(1)∵
∴
由





∴单调递增区间为
(2)







当


知识点
如图在四棱锥P-ABCD中,底面ABCD为直角梯形,AD∥BC,∠ADC=90°,平面PAD垂直底面。Q为AD中点,M是棱PC上的点,PA=PD=2,BC=
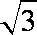
(1)若点


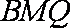
(2)求证:平面PQB
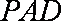
(3)若二面角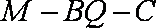
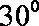
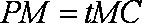
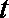
正确答案
见解析
解析
(1)在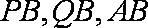


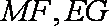
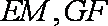
因为底面ABCD为直角梯形,AD∥BC,∠ADC=90°,BC=
于是有: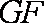
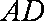


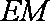
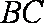
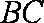
所以,四边形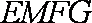
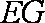
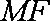

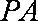
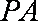
所以,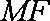
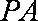
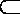
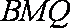

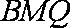
(2)证明:由已知条件得:
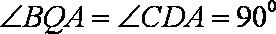
即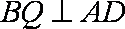
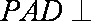


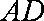
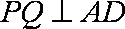
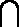
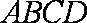
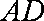
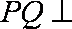
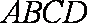
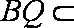
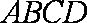
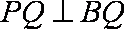
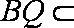
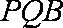
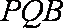

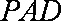
(3)平面PAD⊥底面,而PAD是正三角形,Q为AD中点,
所以PQ⊥AD,PQ⊥底面ABCD,连接CQ,做MN⊥CQ,做NE⊥QB,连ME
MN⊥CQ,PQ⊥CQ,所以MN∥PQ
MN/PQ=CM/CP=1/(1+t) MN=√3/(1+t)
而容易看到BCQD是矩形,NE⊥BQ,所以NE∥BC
NE/BC=QN/QC=t/(1+t) NE=t/(1+t)
二面角就是∠MEN
tan∠MEN=MN/NE=√3/(1+t)/t/(1+t)=√3/t
所以t=3.
知识点
直线



正确答案
解析
圆的方程化为


知识点
已知实数x,y满足
正确答案
[-3,1]
解析
令


在
易知直线


直线

因此
知识点
某品牌的汽车4S店,对最近100位采用分期付款的购车者进行统计,统计结果如下表所示:已知分3期付款的频率为0.2,4S店经销一辆该品牌的汽车,顾客分1期付款,其利润为1万元;分2期或3期付款共利润为1.5万元;分4期或5期付款,其利润为2万元.用
(1)求上表中的a,b值;
(2)若以频率作为概率,求事件A:“购买该器重汽车的3位顾客中,至多有1位采用3期付款”的概率P(A);
(3)求

正确答案
见解析。
解析
(1)由
(2)记分期付款的期数为x,依题意得:
则“购买该品牌汽车的3位顾客中至多有1位采用3期付款”的概率:
(3)∵



∴
∴

知识点
在直三棱柱ABC﹣A1B1C1中,AD⊥平面A1BC,其垂足D落在直线A1B上。
(1)求证:BC⊥A1B;
(2)若
正确答案
见解析。
解析
(1)证明:三棱柱 


又


又











又



(2)在直三棱柱







在



在

由(1)知








知识点







正确答案
解析
由











知识点
若实数x,y满足条件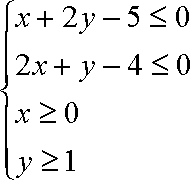
正确答案
解析
做出可行域,由图象可知当目标函数经过直线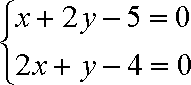
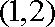
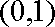
知识点
扫码查看完整答案与解析