- 牛顿运动定律
- 共1024题
如图,粗糙的水平地面上有一斜劈,斜劈上一物块正在沿斜面以速度v0匀速下滑,斜劈保持静止,则地面对斜劈的摩擦力
正确答案
解析
斜劈和物块都平衡对斜劈和物块整体受力分析知地面对斜劈的摩擦力为零,选A。
知识点
随着机动车数量的增加,交通安全问题日益凸显。分析交通违法事例,将警示我们遵守交通法规,珍惜生命。一货车严重超载后的总质量为49t,以54km/h的速率匀速行驶。发现红灯时司机刹车,货车即做匀减速直线运动,加速度的大小为2.5m/s2(不超载时则为5m/s2)。
(1)若前方无阻挡,问从刹车到停下来此货车在超载及不超载时分别前进多远?
(2)若超载货车刹车时正前方25m处停着总质量为1t的轿车,两车将发生碰撞,设相互作用0.1s后获得相同速度,问货车对轿车的平均冲力多大?
正确答案
见解析。
解析
(1)货车刹车时的初速是v0=15vm/s ,末速是0,加速度分别是2.5m/s2和5m/s2,根据位移推论式得
代入数据解得: 超载,

(2)货车与轿车相撞时的速度为

相撞时动量守恒,有

对轿车根据动量定理有

知识点
如图甲所示,在水平面上固定有长为L=2m、宽为d=1m的金属“U”型导轨,在“U”型导轨右侧l=0.5m范围内存在垂直纸面向里的匀强磁场,且磁感应强度随时间变化规律如图乙所示。在t=0时刻,质量为m=0.1kg的导体棒以v0=1m/s的初速度从导轨的左端开始向右运动,导体棒与导轨之间的动摩擦因数为μ=0.1,导轨与导体棒单位长度的电阻均为λ=0.1Ω/m,不计导体棒与导轨之间的接触电阻及地球磁场的影响(取g=10m/s2)。
(1)通过计算分析4s内导体棒的运动情况;
(2)计算4s内回路中电流的大小,并判断电流方向;
(3)计算4s内回路产生的焦耳热。
正确答案
见解析。
解析
(1)导体棒先在无磁场区域做匀减速运动,有
代入数据解得:
导体棒在1s末已经停止运动,以后一直保持静止,离左端位置仍为
(2)前2s磁通量不变,回路电动势和电流分别为
后2s回路产生的电动势为
回路的总长度为
电流为
根据楞次定律,在回路中的电流方向是顺时针方向。
(3)前2s电流为零,后2s有恒定电流,焦耳热为
知识点
倾角θ=37°,质量M=5kg的粗糙斜面位于水平地面上,质量m=2kg的木块置于斜顶端,从静止开始匀加速下滑,经t=2s到达底端,运动路程L=4m,在此过程中斜面保持静止(sin37°=0.6,cos37°=0.8,g取10m/s2),求:
(1)地面对斜面的摩擦力大小与方向;
(2)地面对斜面的支持力大小;
(3)通过计算证明木块在此过程中满足动能定理。
正确答案
(1)地面对斜面的摩擦力大小为3.2N,方向水平向左;
(2)地面对斜面的支持力大小为67.6N;
(3)下滑过程中W=△Ek,动能定理成立。
解析
(1)木块做加速运动L=

对木块由牛顿定律mgsinθ﹣f1=ma
f1=mgsinθ﹣ma=8N,N1=mgcosθ=16N,
对斜面由共点力平衡,地对斜面的摩擦力f2=N1sinθ﹣f1cosθ=3.2N,方向水平向左。
(2)地面对斜面的支持力N2=Mg+N1cosθ+f1sinθ=67.6N,
(3)木块在下滑过程中,沿斜面方向合力及该力做的功为
F=mgsinθ﹣f1=4N,W=FL=16J。
木块末速度及动能增量v=at=4m/s,△Ek=
由此可知下滑过程中W=△Ek,动能定理成立。
知识点
如图所示,间距l=0.3m的平行金属导轨a1b1c1和a2b2c2分别固定在两个竖直面内,在水平面a1b1b2a2区域内和倾角θ=37º的斜面c1b1b2c2区域内分别有磁感应强度B1=0.4T、方向竖直向上和B2=1T、方向垂直于斜面向上的匀强磁场。电阻R=0.3Ω、质量m1=0.1kg、长为l 的相同导体杆K、S、Q分别放置在导轨上,S杆的两端固定在b1、b2点,K、Q杆可沿导轨无摩擦滑动且始终接触良好。一端系于K杆中点的轻绳平行于导轨绕过轻质滑轮自然下垂,绳上穿有质量m2=0.05kg的小环。已知小环以a=6m/s2的加速度沿绳下滑,K杆保持静止,Q杆在垂直于杆且沿斜面向下的拉力F作用下匀速运动。不计导轨电阻和滑轮摩擦,绳不可伸长。取g=10 m/s2,sin37º=0.6,cos37º=0.8。求:
(1)小环所受摩擦力的大小;
(2)Q杆所受拉力的瞬时功率。
正确答案
见解析。
解析
(1)设小环受到摩擦力大小为f,则由牛顿第二定律得到
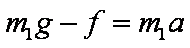
代入数据得到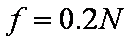
说明:①式3分,②式1分
(2)设经过K杆的电流为I1,由K杆受力平衡得到

设回路总电流为I,总电阻为R总,有

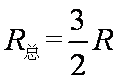
设Q杆下滑速度大小为v,产生的感应电动势为E,有
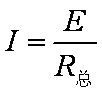
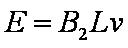
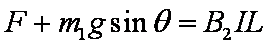
拉力的瞬时功率为P=Fv........⑨
联立以上方程得到P=2W......⑩
知识点
如图,将质量m=0.1kg的圆环套在固定的水平直杆上。环的直径略大于杆的截面直径。环与杆间动摩擦因数μ=0.8。对环施加一位于竖直平面内斜向上,与杆夹角θ=53°的拉力F,使圆环以a=4.4m/s2的加速度沿杆运劝,求F的大小。
正确答案
见解析。
解析
令
当
由牛顿定律
解得
当
由牛顿定律
解得

知识点
如图所示,一质量m=0.4kg的小物块,以V0=2m/s的初速度,在与斜面成某一夹角的拉力F作用下,沿斜面向上做匀加速运动,经t=2s的时间物块由A点运动到B点,A、B之间的距离L=10m。已知斜面倾角θ=30o,物块与斜面之间的动摩擦因数
(1)求物块加速度的大小及到达B点时速度的大小。
(2)拉力F与斜面的夹角多大时,拉力F最小?拉力F的最小值是多少?
正确答案
见解析。
解析
(1)设物块加速度的大小为a,到达B点时速度的大小为v,由运动学公式得


联立以上两式得

(2)设物块所受支持力为

由牛顿第二定律得


又
联立上式得

由数学知识得

由89式可知对应F最小的夹角为 
联立3810式,代入数据得F的最小值为
知识点
如图所示,水平板上有质量m=1.0kg的物块,受到随时间t变化的水平拉力F作用,用力传感器测出相应时刻物块所受摩擦力Ff的大小。取重力加速度g=10m/s2。下列判断正确的是
正确答案
解析
由图可得,物体与地面间的最大静摩擦力为4N,物体从第4秒开始运动,在第4秒-第5秒内发生位移,因此做功不为零;4秒末物块所受合力为0,N;4秒以后,物块所受摩擦力为滑动摩擦力,根据滑动摩擦力公式可求得动摩擦因数为0.3;根据牛顿第二定律可求得加速度为2.0m/s2。此题考查学生对基本的物理情景的分析。
知识点
某兴趣小组用如题25图所示的装置进行实验研究。他们在水平桌面I固定一内径为d的圆柱形玻璃杯,杯口I放置一直径为d ,质量为m 的均匀薄圆板,板内放一质量为2m的物块。板中心,物块均在杯的轴线,则物体与板间动摩擦因数为c,不考虑板与杯口之间的摩擦力,重力加速度为g,不考虑板翻转。
(1)对板施加指向圆心的水平外力F,设物块与板间最大静摩擦力为L,若物块能在板上滑动. 求F应满足的条件
(2)如果对板施加的指向圆心的水平外力是作用时间极短的较大冲击力,冲量为I
① I应满足什么条件才能使物块从板上掉下?
② 物块从开始运动到掉下时的位移s为多少?
③ 根据s与L的关系式,说明要使s更小,冲量应如何改变
正确答案
见解析
解析
解:
(1)设圆板与物块相对静止时,它们之间的静摩擦力为f,共同加速度为a
由牛顿运动定律,有
对物块 f=2ma 对圆板 F-f=ma
两物相对静止,有 f≤fmax
得 F≤
相对滑动的条件 F>
(2)设冲击刚结束时圆板获得的速度大小为v0,物块掉下时,圆板和物块速度大小分别为v1和v2.
由动量定理,有 I=mv0
由动能定理,有
对圆板-2



对物块2

由动量守恒定律,有
mv0=mv1+2mv2
要使物块落下,必须 v1>v2
由以上各式得
I>
s=
分子有理化得
s=
根据上式结果知:I越大,s越小.
知识点
如图,质量




(1)求物体与地面间的动摩擦因数μ;
(2)用大小为30N,与水平方向成37°的力斜向上拉此物体,使物体从A处由静止开始运动并能到达B处,求该力作用的最短时间t。
正确答案
(1) 0.5
(2)1.03s
解析
(1)物体做匀加速运动


由牛顿第二定律



(2)设F作用的最短时间为t,小车先以大小为a的加速度匀加速t秒,撤去外力后,以大小为a’,的加速度匀减速t’秒到达B处,速度恰为0,由牛顿定律

∴

由于匀加速阶段的末速度即为匀减速阶段的初速度,因此有




(2)另解:设力F作用的最短时间为t,相应的位移为s,物体到达B处速度恰为0,由动能定理


由牛顿定律




知识点
扫码查看完整答案与解析