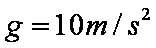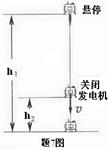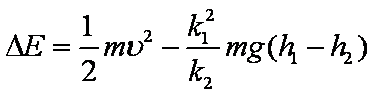- 牛顿运动定律
- 共1024题
近来,我国多个城市开始重点治理“中国式过马路”行为。每年全国由于行人不遵守交通规则而引发的交通事故上万起,死亡上千人。只有科学设置交通管制,人人遵守交通规则,才有保证行人的生命安全。
如下图所示,停车线AB与前方斑马线边界CD间的距离为23m。质量8t、车长7m的卡车以54km/h的速度向北匀速行驶,当车前端刚驶过停车线AB,该车前方的机动车交通信号灯由绿灯变黄灯。
(1)若此时前方C处人行横道路边等待的行人就抡先过马路,卡车司机发现行人,立即制动,卡车受到的阻力为3×104N。求卡车的制动距离?
(2)若人人遵守交通规则,该车将不受影响地驶过前方斑马线边界CD。为确保行人安全,D处人行横道信号灯应该在南北向机动车信号灯变黄灯后至少多久变为绿灯?
正确答案
答案:
解析
已知卡车质量m=8t=8×103kg 、初速度v0=54km/h=15m/s.
(1)从制动到停止,阻力对卡车所做的功为W,由动能定理有
已知卡车所受的阻力f=-3×104N,设卡车的制动距离为 s1 ,有
联立式①②式,代入数据解得:
(2)已知车长 



代入数据解得
知识点
在如图所示的竖直平面内,物体A和带正电的物体B用跨过定滑轮的绝缘轻绳连接,分别静止于倾角θ=370的光滑斜面上的M点和粗糙绝缘水平面上,轻绳与对应平面平行。劲度系数k=5N/m的轻弹簧一端固定在O点,一端用另一轻绳穿过固定的光滑小环D与A相连,弹簧处于原长,轻绳恰好拉直,DM垂直于斜面。水平面处于场强E=5×104N/C、方向水平向右的匀强电场中。已知A、B的质量分别为mA=0.1kg,mB=0.2kg,B所带电荷量q=+4×10-6C。设两物体均视为质点,不计滑轮质量和摩擦,绳不可伸长,弹簧始终在弹性限度内,B电量不变。取g=10m/s2,sin370=0.6,cos370=0.8.
(1) 求B所受摩擦力的大小;
(2) 现对A施加沿斜面向下的拉力F使A以加速度a=0.6m/s2开始作匀加速直线运动。A从M到N的过程中,B的电势能增加了
正确答案
见解析
解析



对A:
对B:
联立两式,代入数据得
(2)物体A从M点到N点的过程中,AB两物体的位移均为s,AB间绳子的张力为T,有
设A在N点时速度为v,受弹簧拉力为

由几何关系知
设拉力F的瞬时功率为P,有
联立解得:
知识点
公路上行驶的两汽车之间保持一定的安全距离。当前车突然停止时,后车司机可以采取刹车措施,使汽车在安全距离内停下而不会与前车相碰。通常情况下,人的反应时间和汽车系统的反应时间之和为1s。当汽车在晴天干燥沥青路面上以108km/h的速度匀速行驶时,安全距离为120m,设雨天时汽车轮胎与沥青路面间的动摩擦因数为晴天时的2/5,若要求安全距离仍为120m,求汽车在雨天安全行驶的最大速度。
正确答案
见解析
解析
设路面干燥时,汽车与地面的动摩擦因数为




式中,m和
设在雨天行驶时,汽车与地面的动摩擦因数为


设在雨天行驶时汽车刹车的加速度大小为a,安全行驶的最大速度为


联立①②③④⑤式并代入题给数据得
知识点
2012年10月,奥地利极限运动员菲利克斯·鲍姆加特纳乘气球升至约39km的高空后跳下,经过4分20秒到达距地面约1.5km高度处,打开降落伞并成功落地,打破了跳伞运动的多项世界纪录,取重力加速度的大小
(1)忽略空气阻力,求该运动员从静止开始下落到1.5km高度处所需要的时间及其在此处速度的大小
(2)实际上物体在空气中运动时会受到空气阻力,高速运动受阻力大小可近似表示为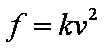
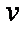
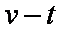
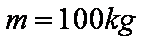
正确答案
见解析
解析
(1)设运动员从开始自由下落至1.5km高度处的时间为t,下落距离为s,在1.5km高度处的速度大小为v,根据运动学公式有:
v=gt ①

依题意有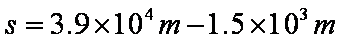
联立①②③可得:t=87s ④
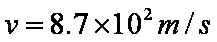
(2)该运动员达到最大速度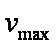
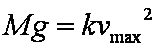
由所给的v-t图像可读出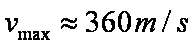
由⑥⑦式可得:
知识点
如图,倾角为37°,质量不计的支架ABCD的D端有一大小与质量均可忽略的光滑定滑轮,A点处有一固定转轴,CA⊥AB,DC=CA=0.3m。质量m=lkg的物体置于支架的B端,并与跨过定滑轮的轻绳相连,绳另一端作用一竖直向下的拉力F,物体在拉力作用下沿BD做匀速直线运动,己知物体与BD间的动摩擦因数μ=0.3。为保证支架不绕A点转动,物体向上滑行的最大距离s=____m。若增大F后,支架仍不绕A点转动,物体能向上滑行的最大距离s′____s(填:“大于”、“等于”或“小于”。)(取sin37°=0.6,cos37°=0.8)
正确答案
0.248 ;
等于
解析
拉力F=mgsin37°+ μmgcos37°=8.4N。BC= CA/ sin37°=0.5m.设m对支架BC的压力mg cos37°对A点的力臂为x,由力矩平衡条件,F·DC cos37°+μmgcos37°·CA cos37°= F·CA cos37°+mg cos37°·x,解得x=0.072m。由x+s=BC-AC sin37°解得s=0.248m。由上述方程可知,F·DC cos37°= F·CA cos37°,x值与F无关,所以若增大F后,支架仍不绕A点转动,物体能向上滑行的最大距离s′=s。
知识点
如图甲所示,静止在水平地面的物块A,受到水平向右的拉力F作用,F与时间t的关系如图乙所示,设物块与地面的静摩擦力最大值fm与滑动摩擦力大小相等,则( )
正确答案
解析
根据图乙可知:在0~t1时间内拉力F没有达到最大静摩擦力fm,物块A处于静止状态,则拉力F的功率为零,A项错误;对物块A由牛顿第二定律有F-fm=ma,由于t2时刻拉力F最大,则t2时刻物块A加速度a最大,B项正确;t2到t3这段时间内拉力F大于fm,所以物块A做加速运动,t3时刻速度达到最大,C项错误、D正确。
知识点
题7图为“嫦娥三号”探测器在月球学科网上着陆最后阶段的示意图。首先在发动机作用下,探测器受到推力在距月面高度为h1处悬停(速度为0,h1远小于月球半径);接着推力改变,探测器开始竖直下降,到达距月面高度为h2处的速度为υ;此后发动机关闭,探测器仅受重力下落到月面。已知探测器总质量为m(不包括燃料),地球和月球的半径比为k1,质量比为k2,地球表面附近的重力加速度为g。求:
(1)月球表面附近的重力加速度大小及探测器刚接触月面时的速度大小;
(2)从开始竖直下降到刚接触月面时,探测器机械能的变化。
正确答案
答案: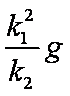
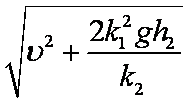
解析
知识点
如图(a),磁铁A、B的同名磁极相对放置,置于水平气垫导轨上。A固定于导轨左端,B的质量m=0.5kg,可在导轨上无摩擦滑动。将B在A附近某一位置由静止释放,由于能量守恒,可通过测量B在不同位置处的速度,得到B的势能随位置x的变化规律,见图(c)中曲线I。若将导轨右端抬高,使其与水平面成一定角度(如图(b)所示),则B的总势能曲线如图(c)中II所示,将B在

(1)B在运动过程中动能最大的位置;
(2)运动过程中B的最大速度和最大位移。
(3)图(c)中直线III为曲线II的渐近线,求导轨的倾角。
(4)若A、B异名磁极相对放置,导轨的倾角不变,在图(c)上画出B的总势能随x的变化曲线。
正确答案
见解析。
解析
(1)势能最小处动能最大(1分)
由图线II得
x=6.1(cm) (2分)
(在5.9 ~ 6.3cm间均视为正确)
(2)由图读得释放处势能

(
最大速度为
(
x=20.0 cm处的总能量为0.90J,最大位移由E=0.90J的水平直线与曲线II的左侧交点确定,由图中读出交点位置为x=2.0cm,因此,最大位移

(
(3)渐近线III表示B的重力势能随位置变化关系,即

由图读出直线斜率



(4)若异名磁极相对放置,A,B间相互作用势能为负值,总势能如图。(2分)
知识点
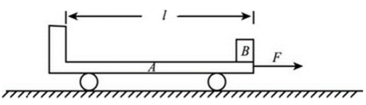
如图所示,水平地面上静止放置一辆小车A,质量mA=4kg,上表面光滑,小车与地面间的摩擦力极小,可以忽略不计。可视为质点的物块B置于A的最右端,B的质量mB=2kg.现对A施加一个水平向右的恒力F=10N,A运动一段时间后,小车左端固定的挡板与B发生碰撞,碰撞时间极短,碰后A、B粘合在一起,共同在F的作用下继续运动,碰撞后经时间t=0.6s,二者的速度达到vt=2m/s.求
(1)A开始运动时加速度a的大小;
(2)A、B碰撞后瞬间的共同速度v的大小;
(3)A的上表面长度l
正确答案
(1)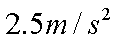
(2)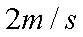
(3)0.45
解析
(1)以A为研究对象,由牛顿第二定律有
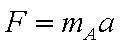
代入数据解得
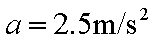
(2)对A,B碰撞后共同运动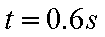
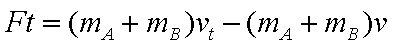
代入数据解得
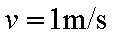
(3)设A,B发生碰撞前,A的速度为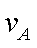
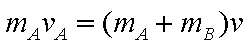
A从开始运动到与B发生碰撞前,由动能定理有
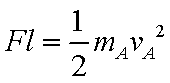
由④⑤⑥式,代入数据解得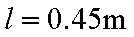
知识点
研究表明,一般人的刹车反应时间(即图甲中“反应过程”所用时间)

(1)减速过程汽车加速度的大小及所用时间;
(2)饮酒使志愿者的反应时间比一般人增加了多少?
(3)减速过程汽车对志愿者作用力的大小与志愿者重力大小的比值。
正确答案
见解析。
解析
(1)设减速过程中汽车加速度的大小为a,所用时间为t,由题可得初速度




联立①②式,代入数据得


(2)设志愿者反应时间为



联立⑤⑥式,代入数据得

(3)设志愿者所受合外力的大小为F,汽车对志愿者作用力的大小为F0,志愿者质量为m,由牛顿第二定律得

由平行四边形定则得

联立③⑧⑨式,代入数据得

知识点
扫码查看完整答案与解析