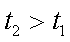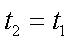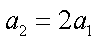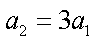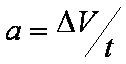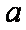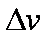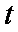- 牛顿运动定律
- 共1024题
如图,一小球通过两细绳固定在圆环的圆心O位置。已知两绳夹角
正确答案
解析
略
知识点
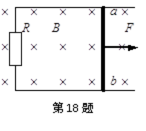
如图,两光滑平行导电导轨水平放置于磁感应强度为B的匀强磁场中,磁场与导轨所在平面垂直,已知金属棒ab能沿导轨自由移动,导轨一端跨接一个定值电阻R,金属棒与导轨电阻均不计,现将金属棒沿导轨以初速度v0开始向右拉动,若保持拉力恒定不变,经过时间t1后金属棒速度变为v,加速度为a1,最终以速度2v做匀速运动,若再使金属棒仍以初速度v0开始,保持拉力的功率不变,经过时间t2后金属棒速度变为v,加速度为a2,最终以速度2v做匀速运动,则
正确答案
解析
略
知识点
对下列物理公式的理解,说法正确的是:
正确答案
解析
略
知识点
如图所示,质量为m的小球A穿在绝缘杆上,细杆的倾角为α,小球A带正电,电荷量为q。在杆上B点处固定一个电荷量为Q的正电荷。将A由距B竖直高度为H处无初速释放,小球A下滑过程中电荷量不变,不计A与细杆间的摩擦,整个装置处于真空中,已知静电力常量k和重力加速度g,求:(1)A球刚释放时的加速度是多大?(2)当A球的动能最大时,A球与B点的距离?(3)若小球到达C点速度最大为v,求A、C两点的电势差UAC?(4)若小球到达D点的速度为0时,A、D两点间的电势差U0,则小球沿杆滑行的位移大小?
正确答案
见解析。
解析
(1)A球刚释放时,受到重力、沿细杆向上的库仑力和细杆的支持力,根据牛顿第二定律得:
得:
(2)到达平衡位置时,速度最大,根据平衡条件,有:
得:
(3)从A到C过程,只有重力和电场力做功,根据动能定理,有:
mgsinα•
将x代入,解得:
(4)从A到D过程,只有重力和电场力做功,设小球沿杆滑行的位移大小为x1,
根据动能定理,有:
mgsinα•x1-q•U0=0

知识点
一个物体在竖直向上的12N的拉力作用下,以2m/s2的加速度向上作匀加速直线运动,如要使加速度增加为4m/s2,空气阻力不计,此竖直拉力的大小应为
正确答案
解析
略
知识点
如图所示,轻线一端系一质量为m的小球,另一端套在图钉A上,此时小球在光滑的水平平台上做半径为a、角速度为ω的匀速圆周运动。现拔掉图钉A让小球飞出,此后细绳又被A正上方距A高为h的图钉B套住,达到稳定后,小球又在平台上做匀速圆周运动。求:
(1)图钉A拔掉前,轻线对小球的拉力大小;
(2)从拔掉图钉A到被图钉B套住前小球做什么运动?所用的时间为多少?
(3)小球最后做圆周运动的角速度。
正确答案
见解析
解析
(1)图钉A拔掉前,轻线的拉力大小为
(2)小球沿切线方向飞出做匀速直线运动直到线环被图钉B套住,小球速度为v=ωa,匀速运动的位移
则时间
(3)v可分解为切向速度v1和法向速度v2,绳被拉紧后v2=0,小球以速度v1做匀速圆周运动,半径r=a+h
由
得
知识点
如图所示,固定的光滑平台上固定有光滑的半圆轨道,轨道半径R=0.6m。平台上静止着两个滑块A、B,mA=0.1Kg,mB=0.2Kg,两滑块间夹有少量炸药,平台右侧有一带挡板的小车,静止在光滑的水平地面上。小车质量为M=0.3Kg,车面与平台的台面等高,车面左侧粗糙部分长度为L=0.8m,动摩擦因数为μ=0.2,右侧拴接一轻质弹簧,弹簧自然长度所在处车面光滑。点燃炸药后,A滑块到达轨道最高点时对轨道的压力大小恰好等于A滑块的重力,滑块B冲上小车。两滑块都可以看作质点,炸药的质量忽略不计,爆炸的时间极短,爆炸后两个物块的速度方向在同一水平直线上,且g=10m/s2。求:
(1)滑块在半圆轨道最低点对轨道的压力
(2)炸药爆炸后滑块B的速度大小
(3)滑块B滑上小车后的运动过程中弹簧的最大弹性势能
正确答案
见解析。
解析
(1)在最高点由牛顿第二定律:
由已知最高点压力
由机械能守恒定律:
在半圆轨道最低点由牛顿第二定律:
解得: 
由牛顿第三定律:
滑块在半圆轨道最低点对轨道的压力大小为7N,方向竖直向下 ……(1分)
(2)由动量守恒定律:

(3)由动量守恒定律:
由能量守恒定律:

知识点
有一质量2kg小球串在长0.5m的轻杆顶部,轻杆与水平方向成
(1)小球下滑的加速度和小球与轻杆之间的动摩擦因数;
(2)如果在竖直平面内给小球施加一个垂直于轻杆方向的恒力,使小球释放后加速度为2m/s2,此恒力大小为多少?
正确答案
见解析
解析
(1)据

另据牛顿第二运动定律有

带入数据可解得
(2)据题意,,根据牛顿第二定律可得:


如果对物体施加垂直与杆子斜向左下方的力F
则有 
解得F=16N
如果对物体施加垂直与杆子斜向右上方的力F

解得
知识点
在足够长的光滑固定水平杆上,套有一个质量为





(1)当子弹射穿木块时,轻绳的拉力大小
(2)当子弹射穿木块后,木块向右摆动的最大高度
(3)当木块第一次返回到最低点时,木块的速度大小
正确答案
见解析。
解析
(1)设子弹从木块中穿出时木块的速度为v1,在子弹与木块相互作用的过程中,由动量守恒:

解得: v1=8m/s
对木块,由牛顿第二定律得:
解得: F = 148N
(2)在木块与圆环一起向右运动的过程中,由水平方向动量守恒,机械能守恒,得:
解得: h = 0.64m
(3)木块从最高点返回最低点的过程中,由水平方向动量守恒、机械能守恒得:
解得: v3 = 12.8m/s
vM = 4.8m/s
v3 = 0
vM = 8m/s
知识点
如图所示,在倾角为θ的光滑斜面上,存在着两个大小相等、方向相反的匀强磁场,磁场方向与斜面垂直,两磁场的宽度MJ和J G均为L,一个质量为m、电阻为R、边长也为L的正方形导线框,由静止开始沿斜面下滑,当ab边刚越过GH进入磁场时,线框恰好以速度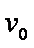
正确答案
解析
略。
知识点
扫码查看完整答案与解析