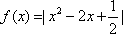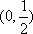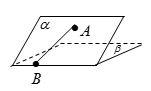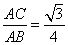- 圆锥曲线与方程
- 共2033题
8.双曲线
A2
B
C
D
正确答案
解析
双曲线
双曲线
可得：
即
故选A.
考查方向
解题思路
先根据双曲线方程求得双曲线的渐近线，进而利用圆心到渐近线的距离为圆的半径求得a和b的关系，进而利用
易错点
直线与圆相切，圆心到直线的距离等于半径.
知识点
12.已知双曲线
正确答案
1 2
解析
由题意渐近线方程为：
因为焦点为
考查方向
解题思路
利用双曲线的几何性质进行计算
易错点
渐近线为 
知识点
请你谈一谈对“不同生产方式以及生产工艺中，生产物流管理所采用的方法和手段是不同的。”这句话的理解。
正确答案
测试
某学校高一年级男生人数占该年级学生人数的40%.在一次考试中，男、女生平均分数分别为75、80，则这次考试该年级学生平均分数为______。
正确答案
78
解析
平均成绩=
知识点
已知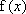
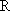
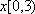
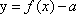
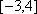
正确答案
解析
根据题目条件，零点问题即转化为数形结合，通过找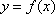
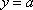
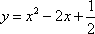
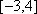
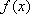
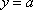
知识点
已知抛物线关于
并且经过点
A
B
C
D
正确答案
解析
设抛物线方程为y2=2px(p>0),则焦点坐标为（
知识点
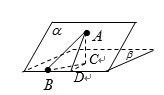
如图，二面角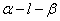
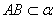
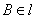
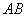
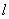
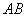
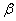
正确答案
解析
过点A作平面β的垂线，垂足为C，在β内过C作l的垂线.垂足为D
连结AD，有三垂线定理可知AD⊥l，
故∠ADC为二面角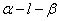
又由已知，∠ABD＝30°
连结CB，则∠ABC为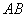
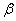
设AD＝2，则AC＝
AB＝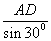
∴sin∠ABC＝
知识点
16.已知
正确答案
解析
解析已在路上飞奔，马上就到！
知识点
6.已知双曲线
A
B
C
D
正确答案
知识点
7. 焦点为
A
B
C
D
正确答案
解析
由所求双曲线与双曲线
考查方向
解题思路
由所求双曲线与已知双曲线共渐近线，设出双曲线方程，利用焦点在y轴上，得到关于
易错点
熟悉双曲线的渐近线与方差之间的关系。
知识点
请你谈一谈对“不同生产方式以及生产工艺中，生产物流管理所采用的方法和手段是不同的。”这句话的理解。
正确答案
测试
设F为抛物线C：y2=3x的焦点，过F且倾斜角为30°的直线交于C于A，B两点，则|AB|=（ ）
A
B6
C12
D7
正确答案
解析
由y2=3x得其焦点F（
设A（x1，y1），B（x2，y2）则x1+x2=
知识点
已知双曲线
A
B
C
D
正确答案
解析
抛物线的焦点 
知识点
某几何体三视图如图所示，则该几何体的体积为（ ）
A8﹣
B8﹣
C8﹣π
D8﹣2π
正确答案
解析
由三视图知：几何体是正方体切去两个
正方体的棱长为2，切去的圆柱的底面半径为1，高为2，
∴几何体的体积V=23﹣2×
知识点
已知向量
A
B
C
D
正确答案
解析
因为
知识点
扫码查看完整答案与解析