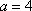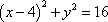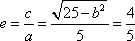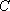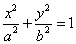- 圆锥曲线与方程
- 共2033题
已知直线











(1)求椭圆
(2)(ⅰ) 设直线



(ⅱ)求线段
正确答案
见解析
解析
(1).椭圆 

(2)(ⅰ)设点

∴

∵点

∴
(ⅱ) 设直线

则

∵
∴ 直线

∴
故
∴
当且仅当

∴


知识点
在平面直角坐标,直线

(1)求椭圆E的方程;
(2)A、B、C是椭圆上的三个动点A与B关于原点对称,且|AC|=|CB|,问△ABC
的面积是否存在最小值?若存在,求此时点C的坐标;若不存在,说明理由。
正确答案
见解析。
解析
知识点
已知动点







正确答案
解析
略
知识点
在平面直角坐标系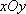

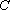
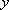
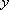
(1)求圆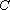
(2)若椭圆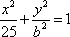


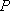
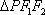
正确答案
见解析。
解析
解:(1)依题意,设圆的方程为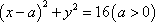
∵圆与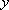
∴圆的方程为
(2)∵椭圆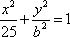
∴
解得
∴
∴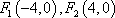
∴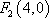
(i)过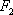

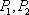

(ii)过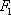
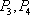
连接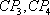
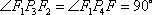
综上,圆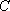
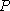
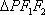
知识点
已知椭圆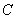
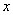
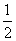
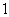
(1)求椭圆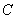
(2)若直线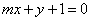

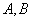
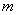
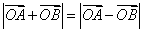
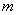
正确答案
见解析
解析
(1)设椭圆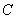
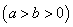

依题意
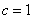
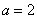
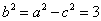
所以椭圆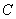

(2)不存在实数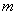
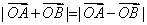
把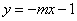
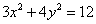
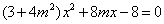
由于直线
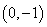
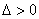
设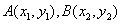
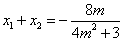
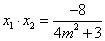
依题意,若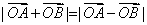
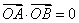
即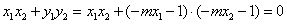
整理得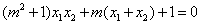
所以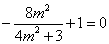
整理得
所以不存在实数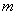

知识点
已知椭圆



(1)求椭圆
(2)若直线







正确答案
(1)
(2)
解析
(1)由已知椭圆的焦点在







(2)






设





设






将



知识点
在极坐标系中,已知圆






正确答案
解析
略
知识点
已知直线








(1)求椭圆
(2)若直线



的值是否为定值,若是求出定值,不是说明理由。
正确答案
见解析。
解析
(1)易知椭圆右焦点

抛物线





∵ 
∴
所以,当


知识点
已知双曲线C:


(1)求椭圆E的方程;
(2)若点P为椭圆的左顶点,

(3)若点P满足|PA|=|PB|,求证
正确答案
见解析。
解析
知识点
如图,已知椭圆E: 





(1)求椭圆E的方程;
(2)求证:点M在直线
(3)是否存在实数

正确答案
见解析
解析
(1)由题意可知


所以,椭圆的标准方程为
(2)设




所以,


于是
因为


(3)设存在这样的平行四边形,则M为OC中点
设点C的坐标为



于是


所以,当

知识点
如图6,椭圆



的两焦点的距离之和为8.
(1)求椭圆
(2)若平行于y轴的直线
的两点


正确答案
见解析。
解析
(2)
知识点
设F1、F2为椭圆的两个焦点,以F2为圆心作圆F2,已知圆F2经过椭圆的中心,且与椭圆相交于M点,若直线MF1恰与圆F2相切,则该椭圆的离心率e为( )
正确答案
解析
易知圆F2的半径为c,(2a-c)2+c2=4c2,(





知识点
已知椭圆

(1)求椭圆E的标准方程;
(2)过椭圆E的左焦点

正确答案
见解析。
解析
知识点
椭圆





(1)求椭圆E及抛物线G的方程;
(2)是否存在学常数


正确答案
见解析。
解析
知识点
已知椭圆的两个焦点和短轴的两个端点恰好为一个正方形的四个顶点,则该椭圆的离心率为
正确答案
解析
略
知识点
扫码查看完整答案与解析