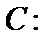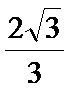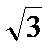- 圆锥曲线与方程
- 共2033题
9. 如图,直线









正确答案
解析
解析已在路上飞奔,马上就到!
知识点
16.已知函数f(x)=sin x- 



正确答案
m≤- 2
解析
∵f'(x)=cos x-

即函数f(x)在(


又不等式f(x)·log2(x-2m+
∴log2(x-2m+


∵
∴2m+

知识点
12.已知x,y的值如下表所示:
如果y与x呈线性相关且回归直线方程为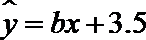
正确答案
0.5
解析
解析已在路上飞奔,马上就到!
知识点
8.若双曲线
正确答案
解析
因为e=

因为x1+x2=-


所以点P(x1,x2)到原点(0,0)的距离d=

知识点
13.如果圆锥曲线
正确答案
解析
若
即-5<λ<2,这时a2=λ+5,b2=2-λ
于是c=

显然焦点在y轴上,得此时的焦点坐标为(0,±
若

这时a2=λ+5,b2=λ-2,于是c=

显然焦点在y轴上,得此时的焦点坐标为(0,±
知识点
7.以抛物线y2=4x的焦点为顶点,顶点为中心,离心率为2的双曲线方程是_______。
正确答案
解析
抛物线的焦点为(1,0),
则双曲线中a=1,且e=
又c2=a2+b2,得b3=3,
则双曲线的方程为
知识点
13.如果圆锥曲线
正确答案
解析
若
即-5<λ<2,这时a2=λ+5,b2=2-λ
于是c=

显然焦点在y轴上,得此时的焦点坐标为(0,±
若

这时a2=λ+5,b2=λ-2,于是c=

显然焦点在y轴上,得此时的焦点坐标为(0,±
知识点
6.到两条互相垂直的异面直线的距离相等的点,在过其中一条直线且平行于另一条直线的平面内的轨迹是( )
正确答案
解析
在边长为a的正方体ABCD-A1B1C1D1中,DC与A1D1是两条互相垂直的异面直线
平面ABCD过直线DC且平行于A1D1,以D为原点
分别以DA,DC所在直线为x轴,y轴建立平面直角坐标系
设点P(x,y)在平面ABCD内,且到A1D1与DC的距离相等
则|x|=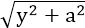
知识点
7.设


正确答案
解析
解析已在路上飞奔,马上就到!
知识点
12.已知双曲线






正确答案
解析
双曲线


故双曲线


所以双曲线

知识点
7.设双曲线

正确答案
解析
由c=1,且焦点在y轴上,得a=2b。A选项不正确,B选项不正确,D选项不正确,所以选C选项。
考查方向
本题主要考查双曲线的标准方程
解题思路
1、求出c;
2、利用a,b,c关系求a,b,即可得到结果。A选项不正确,B选项不正确,D选项不正确,所以选C选项。
易错点
本题易在判断焦点位置时发生错误。
知识点
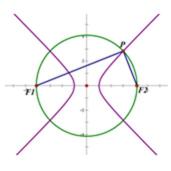
11.设点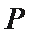
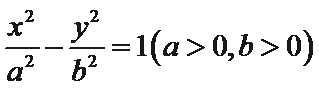
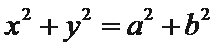
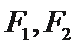
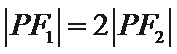
正确答案
解析
根据题意易知圆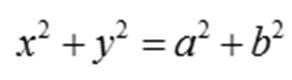
由此可知三角形为直角三角形,因此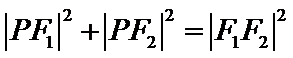
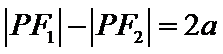
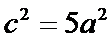
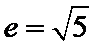
考查方向
解题思路
画出草图,结合图形通过题目条件确定a与c的代数关系,即可求出双曲线的离心率。
易错点
本题容易因为对双曲线的定义不会应用而导致题目不会做。
知识点
如图,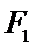
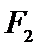
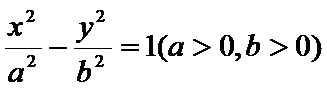
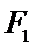
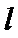
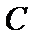
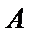
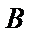
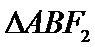
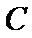
正确答案
解析
因为A、B是双曲线上的点
所以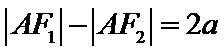
因为是等边三角形,
所以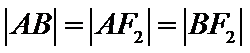
所以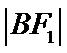
所以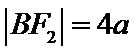
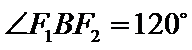
所以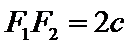
所以根据余弦定理,
可得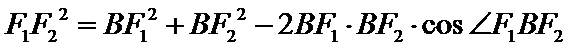
将数据代入得,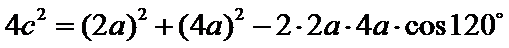
整理得,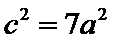
所以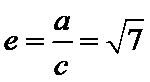
所以选B
考查方向
解题思路
利用双曲线的性质,结合余弦定理求解
易错点
计算能力,想不到利用余弦定理
知识点
10.已知正实数m,n满足:m+n=1,且使



正确答案
解析
由:m+n=1知





考查方向
解题思路
先由均值不等式求出m的值,再求
易错点
均值不等式不会用导致出错。
知识点
7.已知双曲线


正确答案
解析
c2=5+m=9,解得m=4=b2,所以
A选项不正确,B选项不正确,D选项不正确,所以选C选项。
考查方向
解题思路
本题考查双曲线的焦点位置及渐近线方程,解题步骤如下:
1、由题可知,易得x2的系数为负,y2系数为正。
2、c2=5+m=9,解得m=4.
易错点
本题易在求解时把分母平方运算。
知识点
扫码查看完整答案与解析