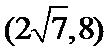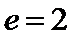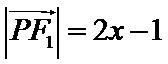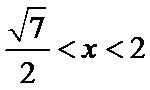圆锥曲线与方程_章节学习

1

题型：填空题

|

填空题 · 5 分

12. 已知双曲线（a＞0，b＞0）的一条渐近线为2x+y=0，一个焦点为（ ,0），则a=_______；b=_____________.

正确答案

a=1， b=2

知识点

双曲线的定义及标准方程

1

题型：填空题

|

填空题 · 4 分

13．设双曲线x2–=1的左、右焦点分别为F1，F2．若点P在双曲线上，且△F1PF2为锐角三角形，则|PF1|+|PF2|的取值范围是_______．

正确答案

．

知识点

双曲线的定义及标准方程

1

题型：填空题

|

填空题 · 5 分

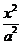
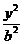
14.已知双曲线E：–=1（a>0，b>0）．矩形ABCD的四个顶点在E上，AB，CD的中点为E的两个焦点，且2|AB|=3|BC|，则E的离心率是_______．

正确答案

2

知识点

双曲线的定义及标准方程双曲线的几何性质

1

题型：填空题

|

填空题 · 5 分

3.在平面直角坐标系xOy中，双曲线的焦距是_______________.

正确答案

知识点

双曲线的定义及标准方程双曲线的几何性质

1

题型：单选题

|

单选题 · 5 分

11. 已知双曲线的两顶点为A1，A2，虚轴两端点为B1，B2，两焦点为F1，F2. 若以A1A2为直径的圆内切于菱形F1B1F2B2，则双曲线的离心率为（）

A

B

C

D

正确答案

A

解析

如下图所示，在三角形OF2B1中，由面积相等可得，整理得，两边同时除以得，即，由解得，选择D选项。

考查方向

本题主要考查了双曲线的方程与性质的综合应用,为高考必考题，在近几年的各省高考题出现的频率较高，常与双曲线的性质、直线与双曲线的位置关系等知识点交汇命题。

解题思路

根据题中条件建立等式，进而求出双曲线的离心率。

易错点

对于已知条件不知如何处理导致出错。

知识点

双曲线的定义及标准方程

1

题型：单选题

|

单选题 · 5 分

7.如图，已知、为双曲线：的左、右焦点，点在第一象限，且满足，，线段与双曲线交于点，若，则双曲线的渐近线方程为( )

A

B

C

D

正确答案

A

解析

由，

可得PF1=F1F2=2C，

由于，，

所以QF2，作F1H⊥PF2于H,

所以：

由双曲线的定义：QF1-QF2=2，QF1

所以选择答案A

考查方向

本题主要考查了圆锥曲线的定义、性质与方程。

解题思路

根据几何性质，找到几何关系，从而利用三角形的性质解决。

易错点

容易将P点看成是双曲线上的点，从而得到：2c=3a。

知识点

双曲线的定义及标准方程

1

题型：填空题

|

填空题 · 5 分

10．已知双曲线的一条渐近线过点，且双曲线的一个焦点在抛物线的准线上，则双曲线的方程为___________

正确答案

解析

将代入渐近线方程，得a=2b. c=,c2=a2+b2, a2+.

考查方向

本题主要考查了双曲线的方程及双曲线与抛物线的基本知识。

解题思路

本题考查运用双曲线的渐近线方程及抛物线的准线方程，求a,b，解题步骤如下：将代入渐近线方程，得a=2b. 由双曲线的一个焦点在抛物线的准线上，可知c=,c2=a2+b2, a2+.

易错点

本题必须注意审题，忽视则会出现错误。

知识点

双曲线的定义及标准方程双曲线的几何性质抛物线的标准方程和几何性质

1

题型：单选题

|

单选题 · 5 分

7.已知双曲线的一个实轴端点与恰与抛物线的焦点重合，且双曲线的离心率等于2，则该双曲线的方程为（）

A

B

C

D

正确答案

D

解析

易知，抛物线焦点坐标为，故，由知，故双曲线的标准方程为，选择D选项。

考查方向

本题主要考查了求双曲线的标准方程，在近几年的各省高考题出现的频率较高，常与椭圆、抛物线等知识点交汇命题。

解题思路

先求出抛物线的焦点坐标，即求出此b，再根据c2=a2+b2即可求出双曲线的标准方程。

易错点

抛物线与双曲线定义不清楚导致出错。

知识点

双曲线的定义及标准方程双曲线的几何性质抛物线的标准方程和几何性质

1

题型：单选题

|

单选题 · 5 分

3．“”是“曲线为双曲线”的（）

A充分而不必要条件

B必要而不充分条件

C充分必要条件

D既不充分也不必要条件

正确答案

A

解析

由题可知，当m>3时，方程我双曲线方程，反之不成立。B选项不正确，C选项不正确，D选项不正确，所以选A选项。

考查方向

本题主要考查双曲线和简易逻辑

解题思路

按照双曲线的标准方程求解B选项不正确，C选项不正确，D选项不正确，所以选A选项。

易错点

本题易在判断条件时发生错误。

知识点

充要条件的判定双曲线的定义及标准方程

1

题型：单选题

|

单选题 · 5 分

A

B

C

D

正确答案

D

知识点

双曲线的定义及标准方程双曲线的几何性质直线、圆及圆锥曲线的交汇问题

1

题型：单选题

|

单选题 · 5 分

5.已知双曲线的一个焦点为,且双曲线的渐近线与圆相切,则双曲线的方程为（）

A

B

C

D

正确答案

D

解析

由双曲线的渐近线与圆相切得,由,解得,故选D.

考查方向

本题考查点到直线的距离公式，双曲线的标准方程，以及双曲线的简单性质的应用，求出a，b的值，是解题的关键．.

解题思路

本题是圆与双曲线的交汇题,虽有一定的综合性,但方法容易想到,仍属于基础题.不过要注意解析几何问题中最容易出现运算错误,所以解题时一定要注意运算的准确性与技巧性,基础题失分过多是相当一部分学生数学考不好的主要原因

易错点

点到直线的距离公式的运用

知识点

双曲线的定义及标准方程

1

题型：填空题

|

填空题 · 4 分

13．设双曲线x2–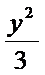=1的左、右焦点分别为F1，F2．若点P在双曲线上，且△F1PF2为锐角三角形，则|PF1|+|PF2|的取值范围是_______．

正确答案

解析

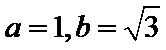
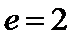
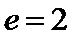
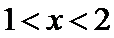
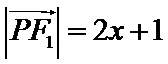
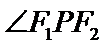
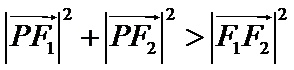
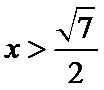
由已知，得，设P（x,y）是双曲线上任一点，由对称性不妨设P在右支上，则，，

由为锐角，则,解得，所以

考查方向

本题主要考查了双曲线的几何性质等知识，为高考题的必考题，在近几年的各省高考题出现的频率较高

解题思路

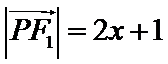
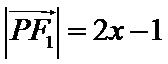
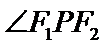
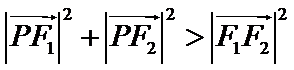
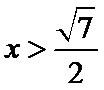
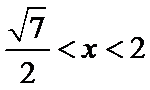
先由题意，，再由为锐角，得则,解得，所以求出即可

易错点

对双曲线的几何性质、锐角三角形的条件不熟悉，计算错误

知识点

双曲线的定义及标准方程

1

题型：简答题

|

简答题 · 14 分

本题共有2个小题，第1小题满分6分，第2小题满分8分.

双曲线的左、右焦点分别为F1、F2，直线l过F2且与双曲线交于A、B两点.

23.若l的倾斜角为，是等边三角形，求双曲线的渐近线方程；

24.设若l的斜率存在，且|AB|=4，求l的斜率.

第(1)小题正确答案及相关解析

正确答案

双曲线的渐近线方程为

解析

解：设．

由题意，，，，

因为是等边三角形，所以，

即，解得．

故双曲线的渐近线方程为．

考查方向

直线与圆锥曲线的位置关系

解题思路

利用等边三角形的性质和双曲线中，得到参数的关系，求出参数

易错点

弦长的运算

第(2)小题正确答案及相关解析

正确答案

斜率为．

解析

解：

由已知，．

设，，直线．

由，得．

因为与双曲线交于两点，所以，且．

由，，得，

故，

解得，故的斜率为．

考查方向

直线与圆锥曲线的位置关系

解题思路

联立方程组，根据弦长公式求出斜率.

易错点

弦长的运算

1

题型：单选题

|

单选题 · 5 分

6．下列双曲线中，渐近线方程为的是（）

A

B

C

D

正确答案

A

解析

由双曲线的渐进线的公式可行选项A的渐进线方程为，故选A.

考查方向

本题主要考查双曲线的渐近线公式.

解题思路

根据选项逐一判断

易错点

求渐近线方程错误，双曲线相关性质掌握不好

知识点

双曲线的定义及标准方程

1

题型：单选题

|

单选题 · 5 分

4.已知双曲线的焦距为，且双曲线的一条渐近线与直线垂直，则双曲线的方程为（）

A

B

C

D

正确答案

A

解析

试题分析：由题得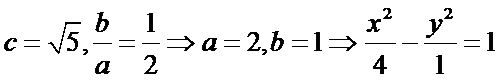，选A.

考查方向

本题主要考查了双曲线的渐近线方程、标准方程等知识点，为高考常考题，在近几年的各省高考题出现的频率较高，常与双曲线的定义、性质等知识点交汇命题。

解题思路

直接根据双曲线的性质即可求出双曲线的标准方程.

易错点

对双曲线的定义记忆不清楚导致出错。

知识点

双曲线的定义及标准方程

热门试卷

正确答案

知识点

正确答案

知识点

正确答案

知识点

正确答案

知识点

正确答案

解析

考查方向

解题思路

易错点

知识点

正确答案

解析

考查方向

解题思路

易错点

知识点

正确答案

解析

考查方向

解题思路

易错点

知识点

正确答案

解析

考查方向

解题思路

易错点

知识点

正确答案

解析

考查方向

解题思路

易错点

知识点

正确答案

知识点

正确答案

解析

考查方向

解题思路

易错点

知识点

正确答案

解析

考查方向

解题思路

易错点

知识点

正确答案

解析

考查方向

解题思路

易错点

正确答案

解析

考查方向

解题思路

易错点

正确答案

解析

考查方向

解题思路

易错点

知识点

正确答案

解析

考查方向

解题思路

易错点

知识点