- 圆锥曲线与方程
- 共2033题
3.在平面直角坐标系
正确答案
解析
考查方向
解题思路
根据双曲线的性质以及
易错点
双曲线中
知识点
15.已知双曲线过点
正确答案
解析
根据双曲线渐近线方程为
考查方向
解题思路
本题是求双曲线的标准方程,若设标准形式,需先判断焦点是在x轴上,还是在y轴上,而此题解法通过设共渐近线的双曲线的方程,就不需要判断双曲线焦点是在x轴上,还是在y轴上.一般的结论是：以
易错点
巧妙设出双曲线方程
知识点
9.将离心率为
长度，得到离心率为
A对任意的
B当
C对任意的
D当
正确答案
解析
不妨设双曲线
考查方向
解题思路
分别表示出离心率再去比较大小。
易错点
计算量大计算不出来。
知识点
13．如图，双曲线C：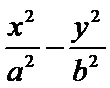
正确答案
解析
考查方向
解题思路
由题意BF垂直于双曲线的渐近线y=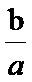
易错点
垂直的关系应用时候出现问题。
知识点
7．已知双曲线
A
B
C
D
正确答案
解析
由渐近线过点
考查方向
解题思路
1、由渐近线所过的点求出
易错点
本题易在等量关系计算上出问题。
知识点
10．双曲线
正确答案
6，
解析
试题分析：依题意可知双曲线的标准方程为
考查方向
解题思路
化双曲线方程为标准方程，直接求出实轴长及渐近线方程，利用直线与圆相切即可求出实数m的值。
易错点
相关知识点不熟悉导致出错。
知识点
6．已知双曲线
曲线的一条渐近线与抛物线的准线的交点坐标为
则双曲线的方程为
A
B
C
D
正确答案
解析
由已知可得
考查方向
解题思路
先画示意图，然后根据双曲线的一条渐近线与抛物线的
准线的交点坐标为
双曲线的方程。
易错点
不会转化为所学内容来做。
知识点
9．设双曲线
A
B
C
D
正确答案
解析
由已知得右焦点
从而
所以
化简得到
故选C.
考查方向
解题思路
本题考查双曲线的简单几何性质，利用向量垂直的条件来转化两直线垂直的条件而得到
易错点
本题属于中档题，注意运算的准确性.
知识点
5.双曲线
A
B
C
D
正确答案
解析
由已知可知，
故选A
考查方向
双曲线的性质，双曲线的渐近线方程
解题思路
根据渐近线方程求出参数的关系，然后求出离心率
易错点
找不到双曲线参数之间的关系
知识点
8.已知抛物线
A
B
C
D
正确答案
解析
根据题意可知，抛物线焦点F(2,0)，因为MF=5,所以
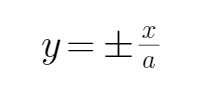
考查方向
双曲线的性质 抛物线的性质
解题思路
设出相关点的坐标，找到等量关系建立方程，然后求出参数。进而得到渐近线方程
易错点
计算能力弱，相关公式记忆混淆
知识点
10.
正确答案
解析
设公共切点的横坐标为
依题意有
两式相除可得
考查方向
导数与切线方程
解题思路
根据导数的集合性质，建立等量关系，然后利用两个等式关系，化简整理求得答案
易错点
不会利用导数求曲线的切线方程
知识点
若实数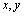
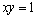
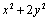
正确答案
解析
由基本不等式可得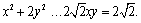
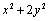
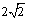
知识点
设a，b是关于t的方程t2cosθ+tsinθ=0的两个不等实根，则过A（a，a2），B（b，b2）两点的直线与双曲线
正确答案
解析
∵a，b是关于t的方程t2cosθ+tsinθ=0的两个不等实根，
∴a+b=﹣
过A（a，a2），B（b，b2）两点的直线为y﹣a2=
即y=﹣
∵双曲线
∴过A（a，a2），B（b，b2）两点的直线与双曲线
知识点
11.设
A
B
C
D
正确答案
解析
可得|PF2|=|F1F2|=2c,故可得|PF1|=4b,则|PF1|-|PF2|=2a,再由b2=c2-a2及e=c/a可得。
考查方向
本题考查双曲线的标准方程和简单几何性质。
解题思路
根据焦点三角形的特征，列a,b,c的方程，转化为e的方程解即可。
易错点
无法得到方程；或解方程错误。
教师点评
本题考查了双曲线的定义，方程，几何性质知识，在近几年的各省高考题出现的频率较高，常与解三角形等知识点交汇命题。
知识点
7. 焦点为
A
B
C
D
正确答案
解析
由所求双曲线与双曲线
考查方向
解题思路
由所求双曲线与已知双曲线共渐近线，设出双曲线方程，利用焦点在y轴上，得到关于
易错点
熟悉双曲线的渐近线与方差之间的关系。
知识点
扫码查看完整答案与解析