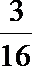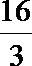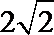- 圆锥曲线与方程
- 共2033题
已知函数
(1)求
(2)若将


正确答案
见解析。
解析
(1)
=
所以

(2)∵将


∴
∵
∴当
当
知识点
若圆锥的内切球与外接球的球心重合,且内切球的半径为
正确答案
解析
过圆锥的旋转轴作轴截面,得△











知识点
双曲线
正确答案
答案:
解析
略
知识点
已知双曲线C:


正确答案
答案:
解析
略
知识点
双曲线2x2﹣y2=﹣1的离心率为( )
正确答案
解析
双曲线2x2﹣y2=﹣1化为标准形式为y2﹣
∴a=1,b=
∴c=

∴e=

知识点
甲.乙两位同学参加2014年的自主招生考试,下火车后两人共同提起一个行李包(如图所示). 设他们所用的力分别为





正确答案
解析
由力的平衡可知

可得




为
知识点
焦点在x轴上的双曲线C的左焦点为F,右顶点为A,若线段FA的中垂线与双曲线C有公共点,则双曲线C的离心率的取值范围是( )
正确答案
解析
设双曲线的方程为 
线段FA的中点坐标为M(
∵线段FA的中垂线与双曲线C有公共点,
∴
则a﹣c≤﹣2a,∴3a≤c,
∴e≥3。
故选D。
知识点
已知双曲线







正确答案
解析
略
知识点
已知圆锥曲线


(1)求曲线
(2)设曲线






(3)在条件(2)下,如果




正确答案
(1)
(2)
(3)m=4
解析
(1)由



故双曲线

(2)设

从而有:
(3)因为
整理得

注意到



设

又




但当
所以
知识点
11.设当x=θ时,函数f(x)=sin x-2cos x取得最大值,则cos θ=_____。
正确答案
解析
略
知识点
10.双曲线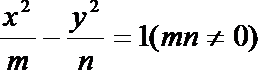
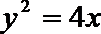
正确答案
解析
解析已在路上飞奔,马上就到!
知识点
9. 从双曲线










正确答案
解析
解析已在路上飞奔,马上就到!
知识点
选做题14、15题,只能选做一题,两题全答的,只计算前一题得分。
14.(坐标系与参数方程选做题)
在极坐标系中,点A的极坐标为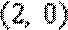
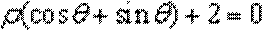
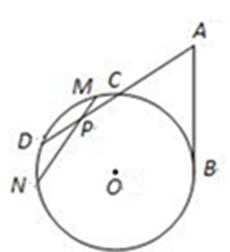
15.(几何证明选讲选做题)
如图所示,过⊙O外一点A作一条直线与⊙O交于C,D两点,AB切⊙O于B,弦MN过CD的中点P.已知AC=4,AB=6,则MP·NP=________.
正确答案
14.
15. 6.25
解析
解析已在路上飞奔,马上就到!
知识点
14.已知圆

正确答案
解析
解析已在路上飞奔,马上就到!
知识点
14.已知双曲线

正确答案
解析
解析已在路上飞奔,马上就到!
知识点
扫码查看完整答案与解析