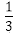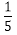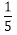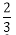- 古典概型的概率
- 共151题
10.已知一个袋子里装有颜色不同的6个小球,其中白球2个,黑球4个,现从中随机取球,每次只取1个球.每次取球后都不放回袋中,取完所有白球就终止游戏,则取球4次游戏结束的概率为（ ）.
A
B
C
D
正确答案
解析
根据题意知,所求事件的概率为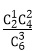
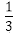
知识点
14.从0,1,2,3,…,9这10个数中任取5个不同的数,则这5个数的中位数是5的概率等于_______.
正确答案
解析
从0,1,2,3,…,9这10个数中任取5个不同的数,共有
知识点
3.从集合{2,3,4,e,
A
B
C
D
正确答案
解析
从集合{2,3,4,e,
共有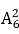
其中满足ab>1,共有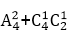
故ab>1的概率为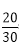
知识点
4.袋中有大小相同的红球和白球各1个,每次任取1个,有放回地摸三次,三次摸到的球恰有两次颜色相同的概率（ ）.
A
B
C
D
正确答案
解析
(法一)摸到红球或白球的概率都是
(法二)所有基本事件为(红,红,红),(红,红,白),(白,红,红),(红,白,红),(白,红,白),(红,白,白),(白,白,红),(白,白,白),共8种.记“三次摸到的球恰有两次颜色相同”为事件A,则A所包含的基本事件为(红,红,白),(白,红,红),(红,白,红),(白,红,白),(红,白,白),(白,白,红),共6种,故P(A)=
知识点
12.两位老师批改同一篇作文,规定批改成绩都是正整数,假设两人批改的成绩都是两位正整数,且十位数字都是5,则两人批改的成绩之差的绝对值不超过2的概率为（ ）.
A
B
C
D
正确答案
解析
设甲的成绩为x,乙的成绩为y,且x,y∈{50,51,52,…,59},
则(x,y)对应如图所示的正方形ABCD内部的整数点,共有10×10=100,
其中满足
故所求概率为P=
知识点
扫码查看完整答案与解析