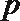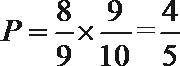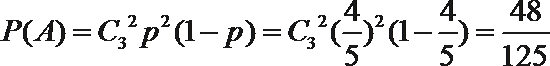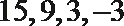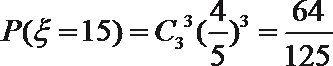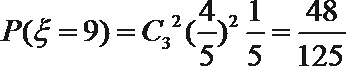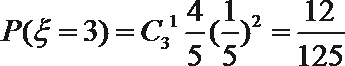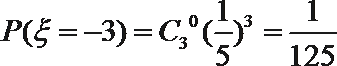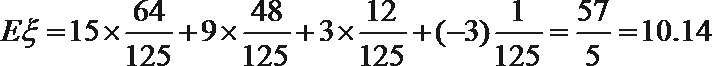- 古典概型的概率
- 共151题
8.春节前,某市一过江大桥上挂了两串彩灯,这两串彩灯的第一次闪亮相互独立,且都在通电后的6秒内任一时刻等可能发生,然后每串彩灯以6秒内间隔闪亮,那么这两串彩灯同时通电后,它们第一次闪亮的时刻相差不超过3秒的概率是( )
正确答案
解析
设两串彩灯分别在通电后x秒,y秒第一次闪亮,
则所有的可能情况对应的平面区域为正方形OABC,
作出直线x﹣y=3和直线y﹣x=3,则两灯在第一次闪亮时刻不超过3秒对应的平面区域为六边形ODEBGF,
∴P=


故选B.
考查方向
解题思路
1、由题意建立几何模型。
2、作出基本事件对应的平面区域和符合条件的平面区域,求出对应的概率。
易错点
本题易在由题意建立几何模型时出错。
知识点
8.学校有两个食堂,现有3名学生前往就餐,则三个人不在同一个食堂就餐的概率是____________.
正确答案
解析
由于学校有两个食堂,不妨令它们分别为食堂A、食堂B,三名学生选择每一个食堂的概率均为




考查方向
本题考查了互斥事件以及相互独立事件的概率,考查学生分析问题的能力.
解题思路
由于学校有两个食堂,不妨令它们分别为食堂A、食堂B,则三名学生选择每一个食堂的概率均为
易错点
混淆互斥事件与相互独立事件.
知识点
15.将一颗骰子投掷两次,第一次出现的点数记为








正确答案
解析
由题可知,P1=1/12,P2=8/9,代入圆的方程得m的取值范围是
考查方向
本题主要考查了概率及直线与圆的综合应用
解题思路
本题考查概率及直线与圆的综合应用,解题思路如下:
1、利用概率公式求出概率;
2、利用直线与圆的综合应用知识求解。
易错点
本题必须注意概率计算
知识点
19.生产甲乙两种元件,其质量按检测指标划分为:
指标大于或者等于


(1)试分别估计元件甲,乙为正品的概率;
(2)生产一件元件甲,若是正品可盈利



在(1)的前提下:
①记

②求生产

正确答案
(1)
(2)66.
解析
试题分析:本题属于概率统计中的基本问题,题目的难度是逐渐由易到难.
解:(1)元件甲为正品的概率约为:
元件乙为正品的概率约为:
(2)①随机变量




而且


所以随机变量
所以:
②设生产的


依题意,
解得:
所以

设“生产


则:
考查方向
本题考查了概率统计中的离散型随机变量的分布列和数学期望的问题.属于高考中的高频考点
解题思路
本题考查概率统计,解题步骤如下:
1、利用已知求出甲、乙为正品的概率。
2、写出随机变量的取值,并求出相应的概率和数学期望
易错点
随机变量的取值及对应的概率。
知识点
17. 某精密仪器生产有两道相互独立的先后工序,每道工序都要经过相互独立的工序检查,且当第一道工序检查合格后才能进入第二道工序,两道工序都合格,产品才完全合格,.经长期监测发现,该仪器第一道工序检查合格的概率为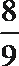
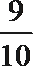
(I)求本月恰有两台仪器完全合格的概率;
(II)若生产一台仪器合格可盈利5万元,不合格则要亏损1万元,记该厂每月的赢利额为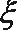
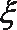
正确答案
解: (Ⅰ) 设恰有两台仪器完全合格的事件为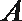
所以
(Ⅱ) 每月生产的仪器完全合格的台数可为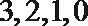
所以赢利额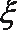
当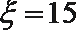
当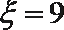
当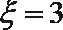
当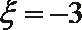
每月的盈利期望
所以每月的盈利期望值为
解析
见答案
考查方向
本题主要考查离散型随机变量的期望与方差,相互独立事件同时发生的概率,属于概率综合题,中档题。
解题思路
第1问直接用公式求解,第2问实际上求的是每月盈利的期望值。
易错点
计算能力弱
知识点
扫码查看完整答案与解析