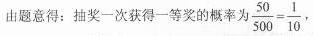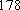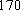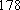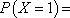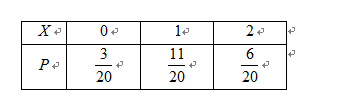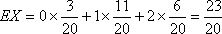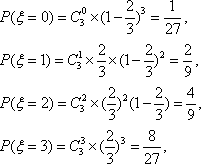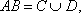- 古典概型的概率
- 共151题
一个盒子里有3个分别标有号码为1,2,3的小球,每次取出一个,记下它的标号后再放回盒子中,共取3次,则取得小球标号最大值是3的取法有()
正确答案
解析
略
知识点
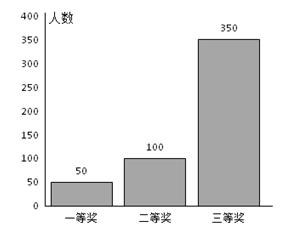
某超市进行促销活动,规定消费者消费每满100元可抽奖一次.抽奖规则:从装有三种只有颜色不同的球的袋中随机摸出一球,记下颜色后放回,依颜色分为一、二、三等奖,一等奖奖金15元,二等奖奖金10元,三等奖奖金5元.活动以来,中奖结果统计如图所示:
消费者甲购买了238元的商品,准备参加抽奖.以频率作为概率,解答下列各题。
(1)求甲恰有一次获得一等奖的概率;
(2)求甲获得20元奖金的概率;
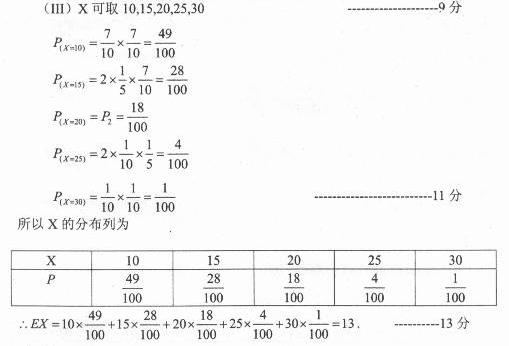
(3)记甲获得奖金金额为X,求X的分布列及期望EX.
正确答案
见解析
解析
知识点
一纸箱中装有大小相等,但编号不同的白色和黄色乒乓球,其中白色乒乓球6个, 黄色乒乓球2个
(1)从中任取2个乒乓球,求恰好取得1个黄色乒乓球的概率;
(2)每次不放回地抽取一个乒乓球,求第1次取得白色乒乓球时已取出黄色乒乓球个数
正确答案
见解析。
解析
(1)
(2)

所以第一次取得白色乒乓球时已取出黄色乒乓球个数的分布列为
知识点
在平面区域





正确答案
解析
由题可知









知识点
现有甲、乙两个靶.某射手向甲靶射击两次,每次命中的概率为

(1)求该射手恰好命中两次的概率;
(2)求该射手的总得分

(3)求该射手向甲靶射击比向乙靶射击多击中一次的概率。
正确答案
见解析
解析
(1)记:“该射手恰好命中两次”为事件



由题意知,
所以

(2)根据题意,





故
……………………8分
所以
(3)设“该射手向甲靶射击比向乙靶射击多击中一次”为事件




所以,该射手向甲靶射击比向乙靶射击多击中一次的概率为
知识点
佛山某中学高三(1)班排球队和篮球队各有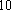
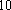
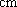
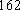
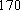
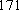
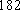
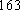
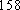
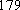
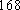
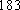
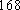
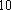
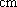
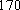
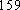
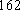
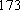
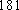
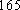
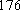
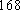
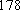
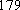
(1) 请把两队身高数据记录在如图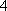
(2) 利用简单随机抽样的方法,分别在两支球队身高超过
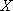
正确答案
见解析。
解析
(1)茎叶图如图所示,篮球队的身高数据方差较小。
(2)排球队中超过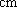
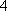
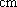

篮球队中超过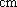

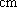
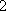
所以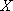
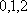
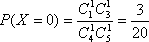
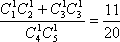
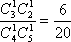
所以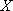
所以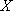
知识点
在一个盒子中,放有标号分别为





(1)求随机变量

(2)求随机变量
正确答案
见解析。
解析
(1)










因此,随机变量




答:随机变量



(2)














则随机变量
因此,数学期望
知识点
甲乙两队参加奥运知识竞赛,每队3人,每人回答一个问题,答对者为本队赢得一分,答错得零分.假设甲队中每人答对的概率均为
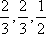
(1)求随机变量ξ分布列和数学期望;
(2)用A表示“甲、乙两个队总得分之和等于3”这一事件,用B表示“甲队总得分大于乙队总得分”这一事件,求P(AB)。
正确答案
见解析
解析
(1)由题意知,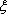
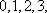
所以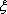
………………………………………………… 5分
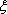

(2)用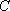
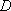
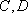
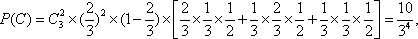
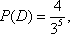
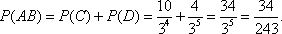
知识点
盒子中装有四张大小形状均相同的卡片,卡片上分别标有数字
(1)在一次试验中,求卡片上的数字为正数的概率;
(2)在四次试验中,求至少有两次卡片上的数字都为正数的概率;
(3)在两次试验中,记卡片上的数字分别为


正确答案
见解析
解析
(1)设事件A:在一次试验中,卡片上的数字为正数,则

答:在一次试验中,卡片上的数字为正数的概率是
(2)设事件B:在四次试验中,至少有两次卡片上的数字都为正数。
由(1)可知在一次试验中,卡片上的数字为正数的概率是
所以
答:在四次试验中,至少有两次卡片上的数字都为正数的概率为
(3)由题意可知,









所以随机变量
所以
知识点
小明从家到学校有两条路线,路线1上有三个路口,各路口遇到红灯的概率均为

(1)若小明上学走路线1,求最多遇到1次红灯的概率;
(2)若小明上学走路线2,求遇到红灯次数
(3)按照“平均遇到红灯次数越少为越好”的标准,请你帮助小明从上述两条路线中选择一条最好的上学路线,并说明理由。
正确答案
见解析
解析
(1)设走路线1最多遇到1次红灯为A事件,则

(2)依题意,



随机变量
………………………………………………9分

(3)设选择路线1遇到红灯次数为

所以
因为
知识点
扫码查看完整答案与解析