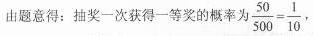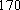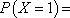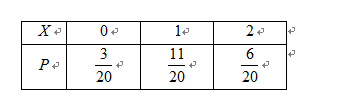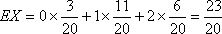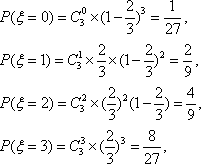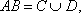- 古典概型的概率
- 共151题
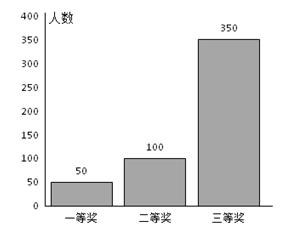
某超市进行促销活动,规定消费者消费每满100元可抽奖一次.抽奖规则:从装有三种只有颜色不同的球的袋中随机摸出一球,记下颜色后放回,依颜色分为一、二、三等奖,一等奖奖金15元,二等奖奖金10元,三等奖奖金5元.活动以来,中奖结果统计如图所示:
消费者甲购买了238元的商品,准备参加抽奖.以频率作为概率,解答下列各题。
(1)求甲恰有一次获得一等奖的概率;
(2)求甲获得20元奖金的概率;
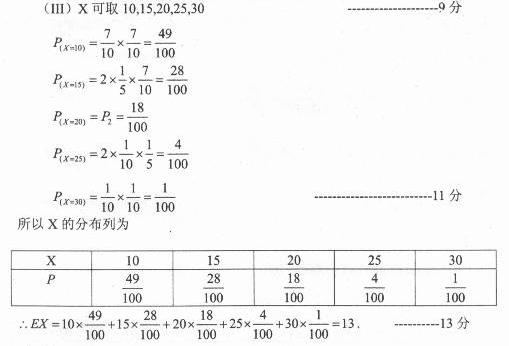
(3)记甲获得奖金金额为X,求X的分布列及期望EX.
正确答案
见解析
解析
知识点
一纸箱中装有大小相等,但编号不同的白色和黄色乒乓球,其中白色乒乓球6个, 黄色乒乓球2个
(1)从中任取2个乒乓球,求恰好取得1个黄色乒乓球的概率;
(2)每次不放回地抽取一个乒乓球,求第1次取得白色乒乓球时已取出黄色乒乓球个数
正确答案
见解析。
解析
(1)
(2)

所以第一次取得白色乒乓球时已取出黄色乒乓球个数的分布列为
知识点
佛山某中学高三(1)班排球队和篮球队各有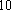
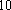
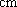
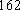
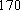
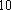
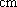
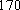
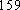
(1) 请把两队身高数据记录在如图
(2) 利用简单随机抽样的方法,分别在两支球队身高超过
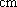
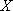
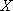
正确答案
见解析。
解析
(1)茎叶图如图所示,篮球队的身高数据方差较小。
(2)排球队中超过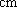
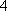
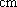

篮球队中超过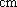

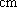
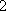
所以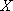
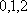
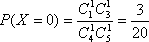
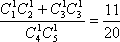
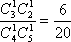
所以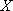
所以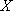
知识点
在一个盒子中,放有标号分别为





(1)求随机变量

(2)求随机变量
正确答案
见解析。
解析
(1)










因此,随机变量




答:随机变量



(2)














则随机变量
因此,数学期望
知识点
甲乙两队参加奥运知识竞赛,每队3人,每人回答一个问题,答对者为本队赢得一分,答错得零分.假设甲队中每人答对的概率均为
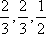
(1)求随机变量ξ分布列和数学期望;
(2)用A表示“甲、乙两个队总得分之和等于3”这一事件,用B表示“甲队总得分大于乙队总得分”这一事件,求P(AB)。
正确答案
见解析
解析
(1)由题意知,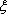
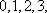
所以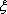
………………………………………………… 5分
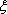

(2)用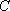
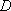
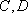
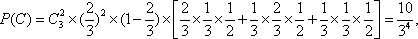
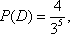
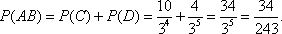
知识点
扫码查看完整答案与解析