- 利用导数求函数的最值
- 共345题
14.已知公差为








正确答案
解析
解析已在路上飞奔,马上就到!
知识点
(1)已知两个等比数列

若数列

(2)是否存在两个等比数列


的等差数列?若存在,求 

正确答案
见解析
解析
(1)












综上:
(2)假设存在这样的等比数列

要使该式成立,则





知识点
设函数f(x)=axn(1-x)+b(x>0),n为正整数,a,b为常数,曲线y=f(x)在(1,f(1))处的切线方程为x+y=1.
(1)求a,b的值;
(2)求函数f(x)的最大值;
(3)证明:
正确答案
见解析
解析
(1)因为f(1)=b,由点(1,b)在x+y=1上,可得1+b=1,即b=0.
因为f′(x)=anxn-1-a(n+1)xn,所以f′(1)=-a.
又因为切线x+y=1的斜率为-1,所以-a=-1,即a=1.故a=1,b=0.
(2)由(1)知,f(x)=xn(1-x)=xn-xn+1,f′(x)=(n+1)·xn-1
令f′(x)=0,解得

在(0,
而在(
故f(x)在(0,+∞)上的最大值为
(3)令φ(t)=ln t-1+
则
在(0,1)上,φ′(t)<0,
故φ(t)单调递减;
而在(1,+∞)上,φ′(t)>0,
故φ(t)单调递增,
故φ(t)在(0,+∞)上的最小值为φ(1)=0,
所以φ(t)>0(t>1),
即ln t>1-
令t=1+

即
所以

由(2)知,
故所证不等式成立。
知识点
已知函数
(1)若曲线




(2)若曲线


正确答案
(1)a=0,b=f(0)=1.
(2)(1,+∞)
解析
由f(x)=x2+xsin x+cos x,得f′(x)=x(2+cos x)。
(1)因为曲线y=f(x)在点(a,f(a))处与直线y=b相切,
所以f′(a)=a(2+cos a)=0,b=f(a),解得a=0,b=f(0)=1.
(2)令f′(x)=0,得x=0.
f(x)与f′(x)的情况如下:
所以函数f(x)在区间(-∞,0)上单调递减,在区间(0,+∞)上单调递增,f(0)=1是f(x)的最小值。
当b≤1时,曲线y=f(x)与直线y=b最多只有一个交点;
当b>1时,f(-2b)=f(2b)≥4b2-2b-1>4b-2b-1>b,
f(0)=1<b,
所以存在x1∈(-2b,0),x2∈(0,2b),使得f(x1)=f(x2)=b.
由于函数f(x)在区间(-∞,0)和(0,+∞)上均单调,所以当b>1时曲线y=f(x)与直线y=b有且仅有两个不同交点。
综上可知,如果曲线y=f(x)与直线y=b有两个不同交点,那么b的取值范围是(1,+∞)。
知识点
已知函数








(1)求

(2)若点



正确答案
(1)
解析
(1)解:由题意得,
因为

又因为
(2)解:设点Q的坐标为(
由题意可知

连接PQ,在△PRQ中,∠PRQ=

解得A2=3,又A>0,所以A=
知识点
已知函数


(1)若曲线



(2)求函数
(3)当



正确答案
见解析
解析
本小题主要考查函数与导数,函数的单调性、极值、零点等基础知识,考查推理论证能力、运算求解能力,考查函数与方程思想、数形结合思想、分类与整合思想、化归与转化思想,满分14分。
(1)由

又曲线


得


(2)
①当




②当







所以


故


综上,当

当



(3)当
令
则直线


等价于方程

假设


又函数





又



所以

解法二:
(1)(2)同解法一。
(3)当

直线


等价于关于




在
①当


②当

令

令

当

当





从而

所以当
解得

综上,得

知识点
△ABC中,点D在边AB上,CD平分∠ACB,若






正确答案
解析
∵ CD为角平分线,∴ 


知识点
已知函数f(x)=axsinx-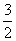
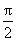
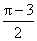
(1)求函数f(x)的解析式;
(2)判断函数f(x)在(0,π)内的零点个数,并加以证明。
正确答案
(1) f(x)=xsinx-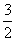
解析
(1)由已知得f′(x)=a(sinx+xcosx),
对于任意x∈(0,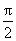
当a=0时,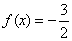
当a<0,x∈(0,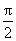
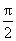
又f(x)在[0,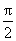
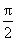
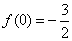
当a>0,x∈(0,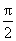
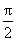
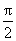
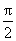
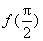
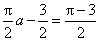
解得a=1。
综上所述,得f(x)=xsinx-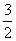
(2)f(x)在(0,π)内有且只有两个零点。
证明如下:
由(1)知,f(x)=xsinx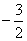
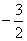
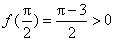
又f(x)在[0,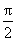
所以f(x)在(0,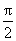
又由(1)知f(x)在[0,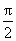
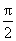
当x∈[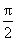
由g(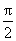
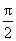
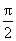
由g′(x)=2cosx-xsinx,知x∈(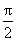
从而g(x)在(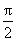
当x∈(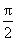
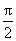
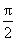
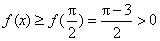
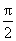
当x∈(m,π)时,有g(x)<g(m)=0,即f′(x)<0,从而f(x)在(m,π)内单调递减。
又f(m)>0,f(π)<0,且f(x)在[m,π]上的图象是连续不断的,从而f(x)在(m,π)内有且仅有一个零点。
综上所述,f(x)在(0,π)内有且只有两个零点
知识点
如图,从A1(1,0,0),A2(2,0,0),B1(0,1,0),B2(0,2,0),C1(0,0,1),C2(0,0,2)这6个点中随机选取3个点。
(1)求这3点与原点O恰好是正三棱锥的四个顶点的概率;
(2)求这3点与原点O共面的概率。
正确答案
(1) 
解析
从这6个点中随机选取3个点的所有可能结果是:
x轴上取2个点的有A1A2B1,A1A2B2,A1A2C1,A1A2C2,共4种,
y轴上取2个点的有B1B2A1,B1B2A2,B1B2C1,B1B2C2,共4种,
z轴上取2个点的有C1C2A1,C1C2A2,C1C2B1,C1C2B2,共4种。
所选取的3个点在不同坐标轴上有A1B1C1,A1B1C2,A1B2C1,A1B2C2,A2B1C1,A2B1C2,A2B2C1,A2B2C2,共8种。
因此,从这6个点中随机选取3个点的所有可能结果共20种。
(1)选取的这3个点与原点O恰好是正三棱锥的四个顶点的所有可能结果有:A1B1C1,A2B2C2,共2种,因此,这3个点与原点O恰好是正三棱锥的四个顶点的概率为
(2)选取的这3个点与原点O共面的所有可能结果有:A1A2B1,A1A2B2,A1A2C1,A1A2C2,B1B2A1,B1B2A2,B1B2C1,B1B2C2,C1C2A1,C1C2A2,C1C2B1,C1C2B2,共12种,因此,这3个点与原点O共面的概率为
知识点
已知函数
(1)当

(2)若存在


正确答案
见解析。
解析
(1)由题意
由


当




所以,

(2) 存在




设此最小值为
(i)当
则

(ii)当
在
在
① 当




② 当




∴
③ 当




综上所述,所求函数的最小值
令
知识点
扫码查看完整答案与解析










































