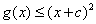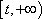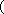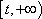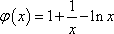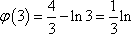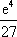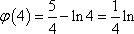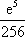- 利用导数求函数的最值
- 共345题
若

(1)当


(2)当



正确答案
见解析。
解析
(1)当


∵


∴函数

故
(2)①当





故当

②当


(i)当



当


(ii)当




故当


(iii)当


故当

综上所述,函数

由



故所求

知识点
已知函数f(x)=-x3+ax2-4(

(1)当a=2时,对于任意的m


(2)若存在

正确答案
见解析。
解析
(1)由题意知
令
当







(2)
①若

又
②若
从而


根据题意,
综上,
(或由
知识点
已知







则


正确答案
8;
解析
略
知识点
设一直角三角形的两条直角边长均是区间

正确答案
解析
设两条直角边长为
知识点
如图,已知P是圆O外一点,PA为 圆O的切线, A为切点,割线PBC经过圆心O,若PA=3
正确答案
解析
略
知识点
函数
正确答案
解析
略
知识点
设函数
(1)若函数
(2)当a=1时,求函数
正确答案
见解析。
解析
(1)∵
∴
令
当x变化时,

故函数
因此



解得

(2)当a=1时,


①当t+3<-1,即t<-4时,
因为


②当

因为





由





③当t+3>2,即t>-1时,
由②得







综上所述,当a=1时,


知识点
已知椭圆


(1)求椭圆的方程;
(2)若点











正确答案
见解析。
解析
(1)由题意可得

∴
所以椭圆的方程为
(2)曲线

设


∵

而


∴
∴点



∴直线

而

∴
∴直线


∴圆心


所以直线

知识点
已知函数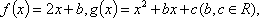
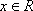
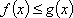
(1)记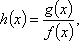
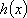
(2)当b=0时,记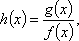
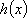
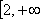
(3)证明:当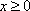
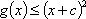
正确答案
见解析
解析
(1)因为任意的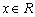
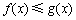
所以对任意的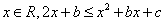
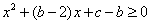
所以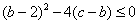
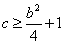
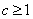
设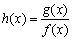
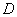
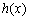
所以对于任意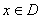
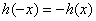
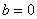
所以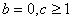
(2)当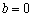
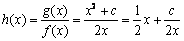
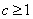
因为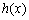
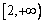
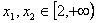
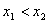
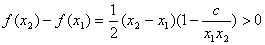
即任取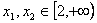
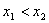
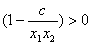
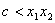
所以
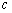
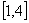
(3)由(1)得,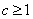
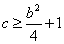
所以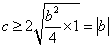
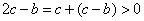
故当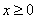
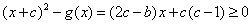
即当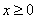
知识点
已知函数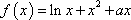
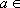
(1)若函数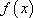

(2)当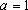

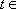
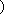

值。
( 参考数值: 自然对数的底数
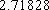
正确答案
见解析。
解析
(1)解法1:函数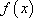
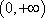
∵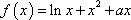
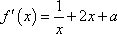
∵ 函数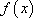
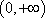
∴ 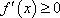
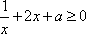
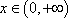
∴ 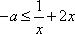
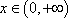
当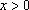
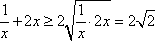
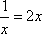
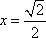
∴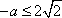
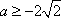
∴
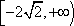
解法2:函数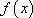
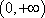
∵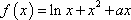
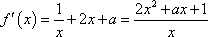
方程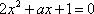
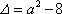
① 当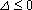
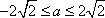
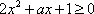
此时, 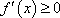
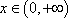
故函数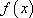
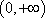
② 当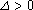
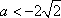
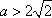
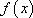
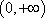
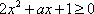
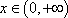
设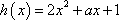
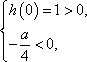
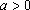
故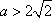
综合①②得
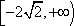
(2)解:当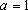
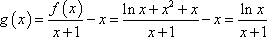
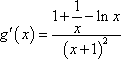
∵ 函数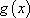
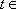
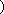
∴ 方程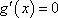
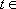
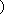
即方程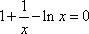
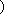
令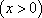
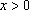
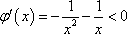
∴函数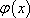
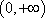
∵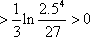
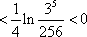
∴函数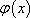
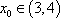
∵方程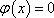
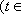
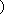
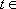
∴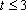
∵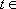

∴

知识点
扫码查看完整答案与解析