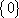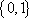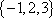- 利用导数求函数的最值
- 共345题
已知函数
(1)若

(2)若



(3)设函数

正确答案
见解析。
解析
(1)由


由



由



(2)由

于是



由

①当




②当

当

由此可得,在

依题意,

综合①②得,实数

由此得,
故
知识点
已知函数
(1)求a的值;
(2)是否存在实数b,使得函数
正确答案
见解析。
解析
(1)由函数




(2)函数


故存在实数:
知识点
向量



正确答案
解析
略
知识点
设



正确答案
-3
解析
略
知识点
已知函数
(1)若


(2)求函数

正确答案
见解析。
解析
(1)因为
所以函数

且
因为

所以
解得
当

当





所以

故
(2)因为
所以
由(1)知
因为

当



所以函数


①当


所以
②当




所以
③当



所以
综上所述:
当



当



当



知识点
某市旅游部门开发一种旅游纪念品,每件产品的成本是





(1)写出

(2)改进工艺后,确定该纪念品的售价,使旅游部门销售该纪念品的月平均利润最大。
正确答案
见解析。
解析
(1)改进工艺后,每件产品的销售价为


∴



(2)由


当



∴函数


故改进工艺后,产品的销售价为
知识点
已知




正确答案
解析
略
知识点
已知定义在R上的函数f(x)满足条件:①对任意的x



正确答案
解析
略
知识点
若函数


正确答案
解析
因为

















知识点
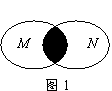
1.已知集合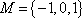
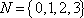
正确答案
解析
阴影部分所示的集合是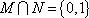
知识点
扫码查看完整答案与解析