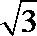- 利用导数求函数的最值
- 共345题
20. 已知函数

(1)当

(2)若函数


(3)若对于任意的



正确答案
解析
解析已在路上飞奔,马上就到!
知识点
13.如下图,在山顶铁塔上B处测得地面上一点A的俯角为



正确答案
解析
解析已在路上飞奔,马上就到!
知识点
9.在极坐标系中,A(1,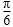
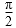
正确答案
解析
解析已在路上飞奔,马上就到!
知识点
21.已知函数

(1)求函数

(2)若存在



正确答案
解析
解析已在路上飞奔,马上就到!
知识点
21. 已知函数



(I)求实数
(II)求

(III)对任意给定的正实数





正确答案
解析
解析已在路上飞奔,马上就到!
知识点
19.请你设计一个LED霓虹灯灯箱.现有一批LED霓虹灯灯箱材料如图所示,ABCD是边长为60 cm的正方形LED散片,边CD上有一以其中点M为圆心,半径为2 cm的半圆形缺损,因此切去阴影部分(含半圆形缺损)所示的四个全等的等腰直角三角形,再沿虚线折起,使得ABCD四个点重合于空间一点P,正好形成一个正四棱柱形状有盖的LED霓虹灯灯箱,E、F在AB上是被切去的等腰直角三角形斜边的两个端点,设AE= FB=xcm.
(1)用规格长×宽×高=145 cm×145 cm ×75 cm外包装盒来装你所设计的LED霓虹灯灯箱,灯箱彼此间隔空隙至多0.5 cm,请问包装盒至少能装多少只LED霓虹灯灯箱(每只灯箱容积V最大时所装灯箱只数最少)?
(2)若材料成本2元/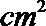
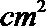

正确答案
解析
解析已在路上飞奔,马上就到!
知识点
22.已知
(1)求

(2)若对一切


正确答案
解析
解析已在路上飞奔,马上就到!
知识点
16.已知函数
(1)求f(x)的最小正周期;
(2)求函数
正确答案
解析
解析已在路上飞奔,马上就到!
知识点
7.函数
正确答案
解析
解析已在路上飞奔,马上就到!
知识点
19. 设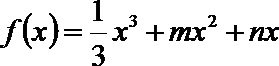
(1)如果
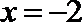
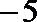
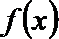
(2)如果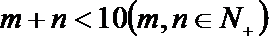
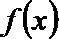
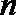
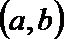
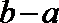
正确答案
解析
解析已在路上飞奔,马上就到!
知识点
扫码查看完整答案与解析