利用导数求函数的最值
共345题

· 利用导数求函数的最值

利用导数求函数的最值
共345题

热门试卷

X 查看更多试卷

题型：简答题

简答题 · 12 分

20.已知函数，

（1）若，求函数的单调区间；

（2）若，且在定义域内恒成立，求实数的取值范围.

正确答案

解析

解析已在路上飞奔，马上就到！

知识点

利用导数研究函数的单调性利用导数求函数的最值利用导数求参数的取值范围

题型：简答题

简答题 · 12 分

20.已知函数，其中

（1）若，求曲线在点的切线方程；

（2）若在区间上，恒成立，求的取值范围。

正确答案

解析

解析已在路上飞奔，马上就到！

知识点

导数的几何意义利用导数求函数的最值利用导数求参数的取值范围

题型：简答题

简答题 · 12 分

20．已知函数f（x）＝a－b＋9x＋2，若f（x）在x＝1处的切线方程为3x＋y－6＝0．

（1）求f（x）的解析式；

（2）若对任意的x∈[ ，2]都有f（x）≥－2t－1成立，求函数g（t）＝＋t－2的最值．

正确答案

解析

解析已在路上飞奔，马上就到！

知识点

导数的几何意义利用导数研究函数的单调性利用导数求函数的最值

题型：填空题

填空题 · 5 分

14．若函数存在最大值M和最小值N, 则M＋N的值为_______．

正确答案

解析

∵函数

令，则有f（x）=1+g（x），且g（x）是奇函数．

故f（x）的最大值M等于g（x）的最大值m加上1，即 M=m+1．

f（x）的最小值N等于g（x）的最小值n加上1，即N=n+1．

再由于g（x）是奇函数，由奇函数的性质可得 m+n=0

故M+N=m+1+n+1=2

知识点

利用导数求函数的最值

题型：填空题

填空题 · 4 分

13．已知函数，则f（x）的最小值为_________.

正确答案

解析

解析已在路上飞奔，马上就到！

知识点

利用导数求函数的最值

题型：简答题

简答题 · 12 分

21．设函数

（I）当a=1时，求函数的极值；

（II）当a≥2时，讨论函数的单调性；

（III）若对任意a∈(2，3)及任意成立，求实数m的取值范围．

正确答案

解析

解析已在路上飞奔，马上就到！

知识点

利用导数研究函数的单调性利用导数求函数的极值利用导数求函数的最值利用导数求参数的取值范围

题型：简答题

简答题 · 14 分

22．设函数，已知，且（a∈R，且a≠0），函数（b∈R，c为正整数）有两个不同的极值点，且该函数图象上取得极值的两点A、B与坐标原点O在同一直线上。

（1）试求a、b的值；

（2）若时，函数的图象恒在函数图象的下方，求正整数的值。

正确答案

解析：（1），∴ ①

又，∴，即 ②

由①②得，．

又时，①、②不成立，故．

∴，设x1、x2是函数的两个极值点，

则x1、x2是方程=0的两个根，，

∴x1+x2=，又∵ A、O、B三点共线， =，

∴=0，

又∵x1≠x2，∴b= x1+x2=，∴b=0．

（2）时，，

由得，可知在上单调递增，在上单调递减，

．①

由得的值为1或2．（∵为正整数） ②

时，记在上切线斜率为2的切点的横坐标为，

则由得，依题意得，

得与矛盾．

（或构造函数在上恒正）

综上，所求的值为1或2．

解析

解析已在路上飞奔，马上就到！

知识点

利用导数求函数的极值利用导数求函数的最值

题型：简答题

简答题 · 13 分

20．已知函数，其中。

（1）当时，讨论函数的单调性；

（2）若函数仅在处有极值，求的取值范围；

（3）若对于任意的，不等式在上恒成立，求的取值范围。

正确答案

解析

解析已在路上飞奔，马上就到！

知识点

利用导数研究函数的单调性利用导数求函数的极值利用导数求函数的最值利用导数求参数的取值范围

题型：简答题

简答题 · 12 分

21．已知函数f（x）＝2lnx－＋ax （a∈R）．

（Ⅰ）当a＝2时，求f（x）的图象在x＝1处的切线方程；

（Ⅱ）若函数g（x）＝f（x）－ax＋m在[，e]上有两个零点，求实数m的取值范围．

正确答案

解析

解析已在路上飞奔，马上就到！

知识点

导数的几何意义利用导数研究函数的单调性利用导数求函数的极值利用导数求函数的最值利用导数求参数的取值范围

题型：简答题

简答题 · 12 分

21.已知函数．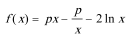

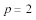
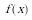
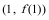
（1）若，求曲线在点处的切线方程；

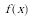
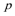
（2）若函数在其定义域内为增函数，求正实数的取值范围；

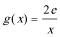
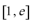
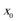
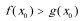
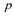
（3）设函数，若在上至少存在一点，使得成立，求实数的取值范围．

正确答案

解析

解析已在路上飞奔，马上就到！

知识点

导数的几何意义利用导数研究函数的单调性利用导数求函数的最值利用导数求参数的取值范围

继续学习学习下一知识点

下一知识点 : 利用导数证明不等式

百度题库 > 高考 > 文科数学 > 利用导数求函数的最值

扫码查看完整答案与解析