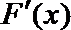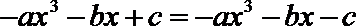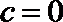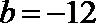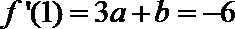- 利用导数求函数的最值
- 共345题
22.已知定义在正实数集上的函数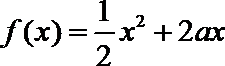
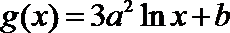
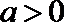
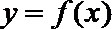
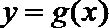
(I)用
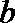
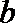
(II)求证: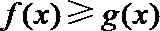
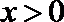
正确答案
(Ⅰ)设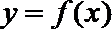
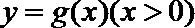
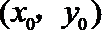
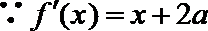
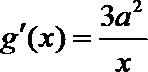
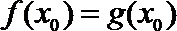
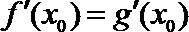
即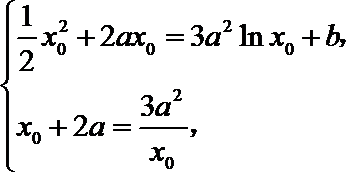
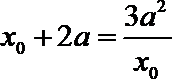
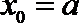
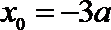
即有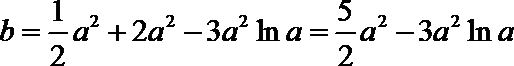
令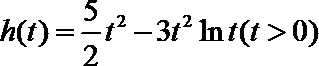
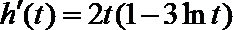
当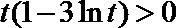
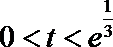
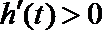
当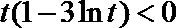
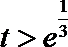
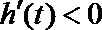
故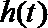
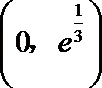
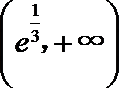
于是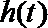
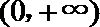
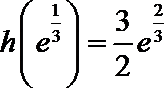
(Ⅱ)设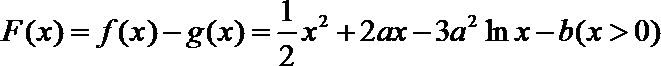
则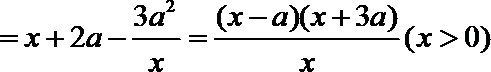
故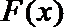
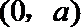
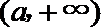
于是函数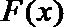
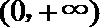
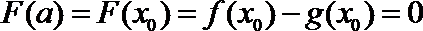
故当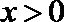
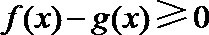
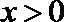
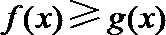
解析
解析已在路上飞奔,马上就到!
知识点
9.函数f(x)=loga|x﹣b|(a>0且a≠1)是偶函数,且在(0,+∞)上单调递减,则f(a﹣3)与f(b﹣2)的大小关系是 _________ .
正确答案
f(a﹣3)<f(b﹣2)
解析
解析已在路上飞奔,马上就到!
知识点
1.抛物线y=4x2的准线方程为 ( )
正确答案
解析
解析已在路上飞奔,马上就到!
知识点
21.已知函数
(1)实数


(2)证明:
正确答案
解析
解析已在路上飞奔,马上就到!
知识点
17.设函数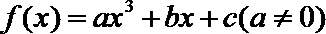
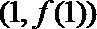
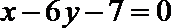
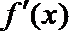
(1)求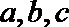
(2)求函数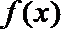
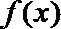
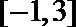
正确答案
(1)∵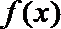
∴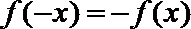
∴
∵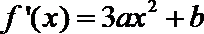
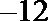
又直线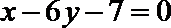

∴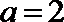
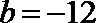
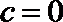
(2)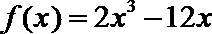
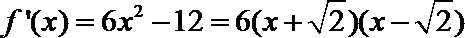
所以函数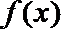
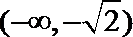
∵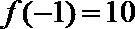
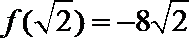
∴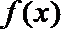
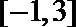
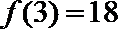
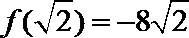
解析
解析已在路上飞奔,马上就到!
知识点
7.若函数



正确答案
解析
解析已在路上飞奔,马上就到!
知识点
16.

正确答案
解析
解析已在路上飞奔,马上就到!
知识点
19.已知函数
(1)求函数
(2)若函数


正确答案
解析
解析已在路上飞奔,马上就到!
知识点
21. 已知函数
(1)当


(2)若在区间



正确答案
解析
解析已在路上飞奔,马上就到!
知识点
10.若存在区间








正确答案
解析
解析已在路上飞奔,马上就到!
知识点
扫码查看完整答案与解析