- 利用导数求函数的最值
- 共345题
11.已知幂函数


正确答案
解析
解析已在路上飞奔,马上就到!
知识点
5.如图,网格纸上小正方形的边长为1,粗线画出的是某多面体的三视图,则该几何体的各个面中最大面的面积为( )
正确答案
解析
解析已在路上飞奔,马上就到!
知识点
22. 已知函数
(I)当


(II)在区间



正确答案
(I)当


曲线


所以曲线


(II)解1:
当




故



当

若

若

所以

因此有

解得
这与
当




所以



综上所述,

解2:有已知得:
设







解析
解析已在路上飞奔,马上就到!
知识点
18. 已知

(1)当


(2)求

正确答案
(1)当


所以

即曲线



所以曲线


即
(2)因为

令

①若




②若




当



所以当


③若




所以当


综上可知,当


当



当



解析
解析已在路上飞奔,马上就到!
知识点
23.设数列





(I)当



(II)当





(III)当










正确答案
(I)当



用


②—①得,

在①中令



∴数列
∴
(II)当



用


④—③得,

用


⑥—⑤得,
即
∴数列
∵

∴公差
∴
(III)由(II)知数列
∵

又对任意
必存在

得

又由已知,

一方面,当

对任意

另一方面,当


则
取

当



∴
解析
解析已在路上飞奔,马上就到!
知识点
5.已知


正确答案
解析
解析已在路上飞奔,马上就到!
知识点
22.已知函数

(1)求函数
(2)若对于区间



(3)若过点


正确答案
(1)
根据题意,得
解得
(2)令
f(-1)=2, f(1)=-2,

则对于区间[-2,2]上任意两个自变量的值
所以

(3)设切点为



则
即
因为过点

所以方程
即函数
则
令


解析
解析已在路上飞奔,马上就到!
知识点
16.若函数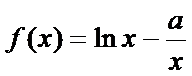
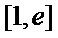
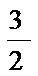
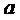
正确答案
解析
解析已在路上飞奔,马上就到!
知识点
22. 已知

(1)

(2)是否存在实数


(3)在(1)的条件下,求证:
正确答案
(1)
减区间
极小值
(2)










所以存在
(3)



而
解析
解析已在路上飞奔,马上就到!
知识点
3.函数
正确答案
解析
解析已在路上飞奔,马上就到!
知识点
扫码查看完整答案与解析