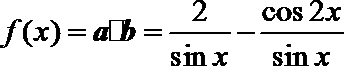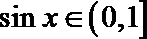- 利用导数求函数的最值
- 共345题
8.下列关于函数
①
② 

③
④ 
正确答案
解析
解析已在路上飞奔,马上就到!
知识点
19.已知

(1)若

(2)若


正确答案
(1) 

(2) 


解析
解析已在路上飞奔,马上就到!
知识点
5.先后抛掷两枚均匀的正方体骰子(它们的六个面分别标有点数1、2、3、4、5、6),骰子朝上的面的点数分别为X、Y,则
正确答案
解析
解析已在路上飞奔,马上就到!
知识点
22. 已知函数

(1)证明:函数



(2)若函数





正确答案
(1)证明:任取




所以

函数

(2)解:因为函数







易知













故
当



又

当



综上所述,

解析
解析已在路上飞奔,马上就到!
知识点
22.选考题:请考生在第22、23、24题中任选一题做答,如果多做,则按所做的第一题记分。
23. 选修4-4:几何证明选讲
在曲线



24.选修4-5:不等式选讲
已知|x-4|+|3-x|
(1)若不等式的解集为空集,求a的范围
(2)若不等式有解,求a的范围
正确答案
22.选修4-1:几何证明选讲
如图,AB是⊙O的直径 ,AC是弦 ,∠BAC的平分线AD交⊙O于点D,DE⊥AC,

(1)求证:DE是⊙O的切线;
(2)若

正确答案
正确答案
17. 已知向量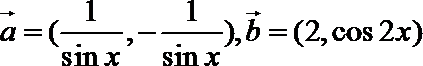
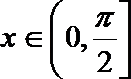
(1)试判断向量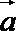
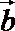
(2)求函数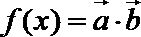
正确答案
(1)若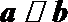
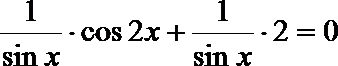
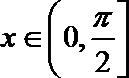
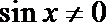
∴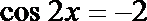
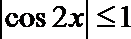
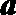
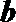
(2)∵
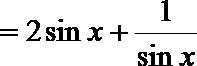
∵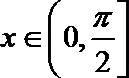
∴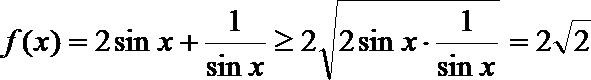
当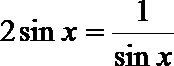
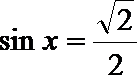
故函数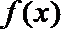
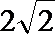
解析
解析已在路上飞奔,马上就到!
知识点
5.函数



正确答案
解析
解析已在路上飞奔,马上就到!
知识点
6.若函数


正确答案
解析
解析已在路上飞奔,马上就到!
知识点
12.若函数


正确答案
解析
解析已在路上飞奔,马上就到!
知识点
10.在各项均为正数的等比数列


正确答案
(-∞,-1]∪[3,+∞]
解析
解析已在路上飞奔,马上就到!
知识点
扫码查看完整答案与解析