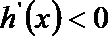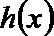- 利用导数求函数的最值
- 共345题
4.设平面区域D是由双曲线



正确答案
解析
解析已在路上飞奔,马上就到!
知识点
7.已知函数







正确答案
解析
解析已在路上飞奔,马上就到!
知识点
18.已知函数


(1)求函数
(2)若经过点


正确答案
解:(1)
根据题意,得

所以
(2)设切点为


则


∵过点

∴方程
∴函数
∴
则



由


解析
解析已在路上飞奔,马上就到!
知识点
1.若全集
正确答案
解析
解析已在路上飞奔,马上就到!
知识点
14.已知M是曲线

正确答案
解析
解析已在路上飞奔,马上就到!
知识点
21.已知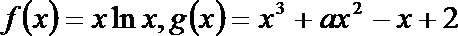
(I)如果函数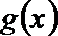
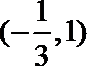
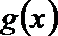
(II)在(Ⅰ)的条件下,求函数y=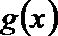
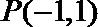
(III)若不等式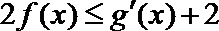
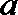
正确答案
解: (I)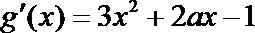
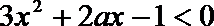
即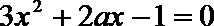
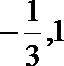
将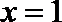
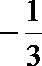
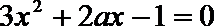
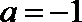
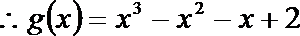
(II)由(Ⅰ)知: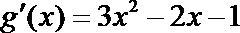
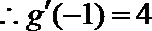
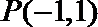
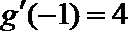
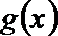
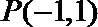
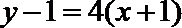
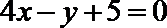
(III)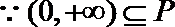
即: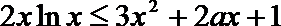
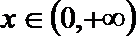
可得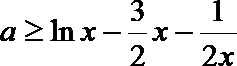
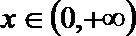
设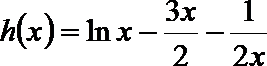
令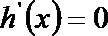
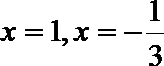
当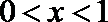
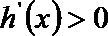
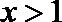
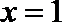
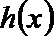
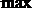
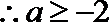
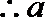
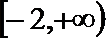
解析
解析已在路上飞奔,马上就到!
知识点
16.已知函数f(x)=x2-x+alnx
(1)当


(2)讨论
正确答案
解析
解析已在路上飞奔,马上就到!
知识点
19.已知各项均为正数的数列

(1)求数列
(2)若
正确答案
(1)
数列
(2)
解析
解析已在路上飞奔,马上就到!
知识点
11.如图,正方体


正确答案
解析
解析已在路上飞奔,马上就到!
知识点
1.若复数
正确答案
解析
解析已在路上飞奔,马上就到!
知识点
扫码查看完整答案与解析