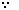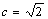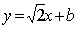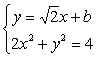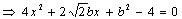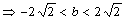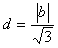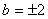- 利用导数求函数的最值
- 共345题
已知函数






(1)求

(2)求数列
(3)若

正确答案
见解析
解析
(1)在


在


(2)在


得

所以



…………6分
(3)数列
令

显然

所以当



当



…………13分
知识点
已知函数


(1)求实数
(2)设
①若


②是否存在点



正确答案
见解析
解析
(1)








(2)①



在
令

设






②由


表明:若点


而线段



这也表明存在点


则这两个封闭图形面积相等, ————13分
知识点
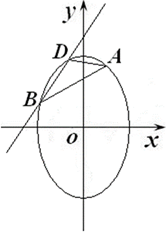
已知点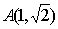
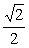

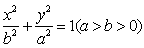

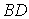
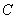
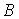
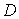
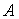

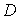
(1)求椭圆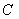
(2)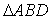
正确答案
见解析。
解析
(1)

∴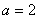
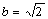
∴椭圆方程为
(2)设直线BD的方程为
∴
∴
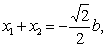
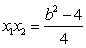
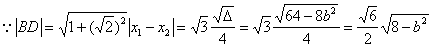
设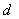
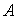
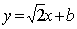
∴
∴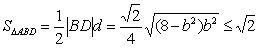

知识点
已知椭圆





(1)求椭圆
(2)过椭圆右焦点F2斜率为














正确答案
见解析。
解析
(1)由题意得

所以


(2)设过点


设点

将直线

整理得:
因为点


且

直线


令


所以点

直线

将
所以

知识点
如图,已知直线l:y=k(x+1)(k>0)与抛物线C:y2=4x相交于A、B两点,且A、B两点在抛物线C准线上的射影分别是M、N,若|AM|=2|BN|,则k的值是
正确答案
解析
略
知识点
扫码查看完整答案与解析