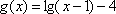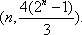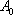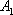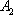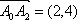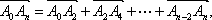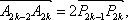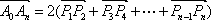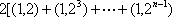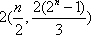- 利用导数求函数的最值
- 共345题
已知函数

(1)求
(2)曲线


正确答案
见解析
解析
(1)
(i)当



(ii)当


令

令,得
∴


在
(2)由(1)知,
(i)当


(ii)当



此时题设成立等价条件是

即:
即:

解得:
由(i)(ii)可知

知识点
在直角坐标系平面中,已知点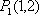
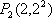
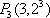
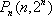

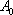
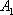
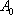
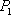
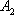
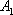

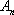

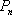
(1)求向量
(2)当点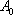

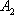
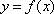

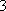
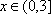
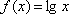

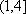
(3)对任意偶数


正确答案
(1)
(2)
(3)
解析
(1)设点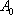
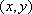
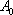
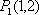
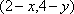

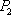
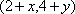
∴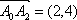
(2)解法1:∵
∴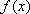
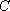
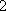
再向上平移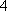
∴曲线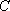
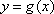
其中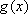

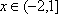
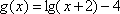
于是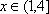
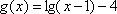
解法2:设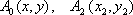

若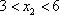

∴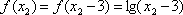
当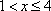
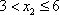

∴当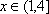
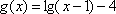
(3)
∵
∴
=
=
=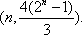
知识点
在



(1)求角C的大小;
(2)若

正确答案
见解析。
解析
(1)由

即


而


(2)






由余弦定理可得
由①②③式可得c=6………12分
知识点
“


正确答案
解析
略
知识点
函数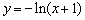
正确答案
解析
略
知识点
扫码查看完整答案与解析