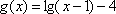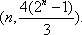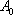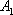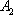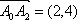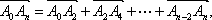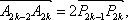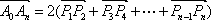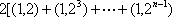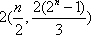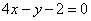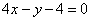- 利用导数求函数的最值
- 共345题
已知函数

(1)求
(2)曲线


正确答案
见解析
解析
(1)
(i)当



(ii)当


令

令,得
∴


在
(2)由(1)知,
(i)当


(ii)当



此时题设成立等价条件是

即:
即:

解得:
由(i)(ii)可知

知识点
现有一组互不相同且从小到大排列的数据

记



(1)求

(2)设直线


(3)证明:当

正确答案
见解析
解析
(1)解:

(2)解:

因为 
所以 
(3)证:由于



事实上,当

下面证明
法一:对任何



所以 
法二:对任何
当

当
综上,
知识点
在直角坐标系平面中,已知点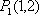
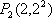
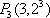
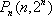

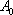
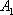
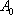
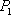
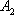
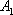

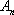

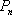
(1)求向量
(2)当点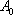

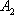
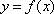

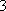
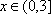
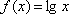

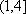
(3)对任意偶数


正确答案
(1)
(2)
(3)
解析
(1)设点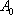
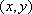
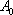
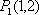
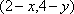

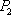
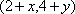
∴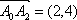
(2)解法1:∵
∴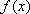
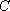
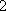
再向上平移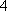
∴曲线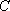
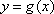
其中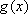

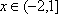
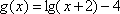
于是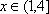
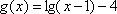
解法2:设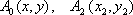

若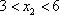

∴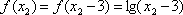
当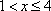
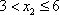

∴当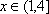
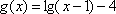
(3)
∵
∴
=
=
=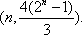
知识点
在



(1)求角C的大小;
(2)若

正确答案
见解析。
解析
(1)由

即


而


(2)






由余弦定理可得
由①②③式可得c=6………12分
知识点
“


正确答案
解析
略
知识点
函数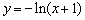
正确答案
解析
略
知识点
学校游园活动有一个游戏项目:箱子里装有3个红球,2个白球,这些球除颜色外完全相同.每次游戏从箱子里摸出3个球,若摸出的是3个红球为优秀;若摸出的2个红球1个白球为良好;否则为合格.
(1)求在1次游戏中获得优秀的概率;
(2)求在1次游戏中获得良好及以上的概率
正确答案
见解析。
解析
知识点




正确答案
解析
略
知识点
某中学高中一年级有



正确答案
解析
略
知识点
曲线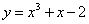
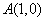

正确答案
解析
略
知识点
扫码查看完整答案与解析