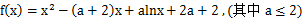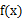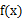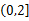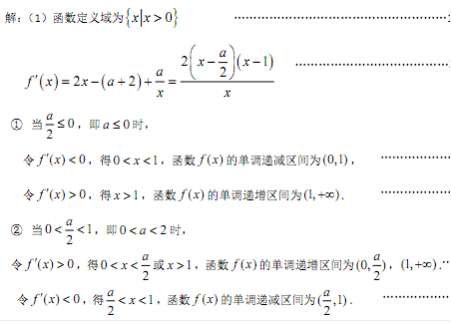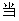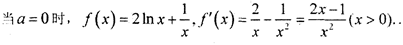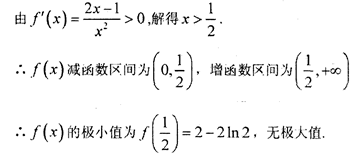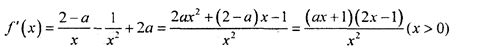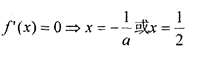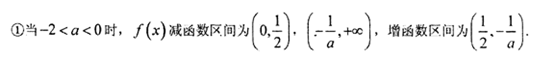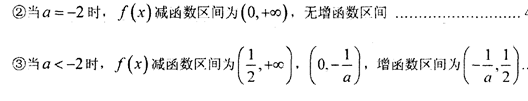- 利用导数求函数的最值
- 共345题
已知函数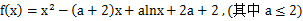
求函数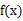
若函数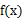
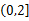

正确答案
见解析。
解析
知识点
已知函数

(1)讨论函数
(2)若函数




正确答案
见解析
解析
(1)在区间

①若



②若


在区间


在区间


综上所述,①当


②当



(2)因为函数

解得
由已知

令

易得


所以

知识点
某四棱锥的三视图如图所示,则最长的一条侧棱长度是( )
正确答案
解析
略
知识点
已知函数





(1)求
(2)若函数

正确答案
见解析。
解析
(1)由





又∵曲线


由<1><2><3>可求得,
(2)若函数




∴方程
解得:

所以当实数


知识点
已知函数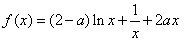
(1)当
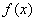
(2)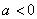
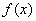
(3)若对任意的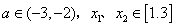
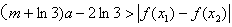
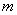
正确答案
见解析。
解析
(1)解:
(2)
知识点
扫码查看完整答案与解析