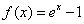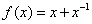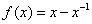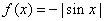- 利用导数求函数的最值
- 共345题
一个几何体的三视图如图所示,则该几何体的体积是
正确答案
解析
该几何体是一个长方体在左边挖去一个三棱柱再拼接到右边而得到的,它的体积就是长方体的体积,体积为
知识点
记直线




正确答案
解析
略
知识点
已知函数
(1)当a=1时,∃x0∈[1,e]使不等式f(x0)≤m,求实数m的取值范围;
(2)若在区间(1,+∞)上,函数f(x)的图象恒在直线y=2ax的下方,求实数a的取值范围。
正确答案
见解析。
解析
(1)当a=1时,
可知当x∈[1,e]时f(x)为增函数,
最小值为
要使∃x0∈[1,e]使不等式f(x0)≤m,即f(x)的最小值小于等于m,
故实数m的取值范围是
(2)已知函数
若在区间(1,+∞)上,函数f(x)的图象恒在直线y=2ax的下方,
等价于对任意x∈(1,+∞),f(x)<2ax,
即
设
即g(x)的最大值小于0.
(1)当

∴
∴g(1)=﹣a﹣
∴a≥﹣
∴
(2)a≥1时,

g(x)无最大值,即最大值可无穷大,故此时不满足条件。
(3)当


同样最大值可无穷大,不满足题意,综上,实数a的取值范围是
知识点
已知函数
(1)求函数
(2)求函数


(3)设函数







正确答案
见解析。
解析
知识点
有两位射击运动员在一次射击测试中各射靶10次,每次命中的环数如下:
则下列判断正确的是
正确答案
解析
略
知识点
已知函数

(1)求
(2)在








正确答案
(1)
(2)
解析
(1)
由已知点



(2)因为
所以

所以

因为


又因为


所以

所以

知识点
设函数
(1)已知曲线




(2)讨论函数
(3)在(1)的条件下,求证:对于定义域内的任意一个

正确答案
见解析
解析
(1)


根据题意,
所以

解得
(2)
1)当



所以


2)当
若




若





综上所述,当







(3)由(1)可知
设


当






可见
所以



知识点
下列函数在其定义域内,既是奇函数又存在零点的是:
正确答案
解析
略
知识点
设函数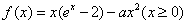
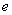
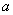
(1)若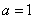
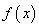
(2)当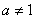
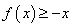
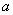
正确答案
见解析。
解析
解:
知识点
已知函数f(x)=

(1)求数列{an}的通项公式an;
(2)令
(3)令cn=


正确答案
见解析。
解析
(1)∵点(n,Sn)(n∈N*)均在函数y=f(x)的图象上,
∴
∴当n=1时,
当n≥2时,an=Sn﹣Sn﹣1=
当n=1时,也适合上式,
因此
(2)由(1)可得:

∴Tn=

两式相减得

∴
(3)证明:由cn=



∴c1+c2+…+cn>2n。
又cn=



∴c1+c2+…+cn=2n+[(








∴2n<c1+c2+…+cn<2n+
知识点
扫码查看完整答案与解析