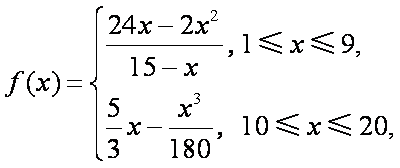- 利用导数求函数的最值
- 共345题
如果实数


正确答案
解析
用数形结合法,设







知识点
设

正确答案
解析


知识点
一动圆与圆

(1)求动圆圆心

(2)设过圆心









正确答案
见解析。
解析
(1)设动圆圆心为

由题意,得


由椭圆定义知






(2)
如图,设


则三角形
=
当


设



由

解得

∴



有


当





即当





∴存在直线


知识点
如图,现要在边长为






.
(1)求


(2)若中间草地的造价为






正确答案
见解析。
解析
(1)由题意得,
解得

(2)记“环岛”的整体造价为

令

由


列表如下:
所以当

答:当
知识点
已知复数

(1)若




(2)设复数




正确答案
(1)
解析
解析:(1)由


∴

故

(2)
由

又

故

又由

故

知识点
如果

正确答案
1
解析
略
知识点
在平面直角坐标系











(1)求椭圆
(2)若点


(3)若


正确答案
见解析。
解析
由题意得
所以椭圆的方程为
(2)因为P(0,1),F1(-1,0),所以PF1的方程为x-y+1=0。
由


解法一:因为kPF·kPF=-1,所以△PQF2为直角三角形。
因为QF2的中点为

所以圆的方程为
解法二:设过P,Q,F2三点的圆为x2+y2+Dx+Ey+F=0,
则
所以圆的方程为
(3)解法一:设P(x1,y1),Q(x2,y2),则
所以

所以
因为


所以


解法二:当PQ斜率不存在时,
在

所以

当PQ斜率存在时,设为k,则PQ的方程是y=k(x+1),
由
韦达定理
设P(x1,y1),Q(x2,y2) ,
则

知识点
根据统计资料,某工艺品厂的日产量最多不超过20件,每日产品废品率
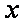
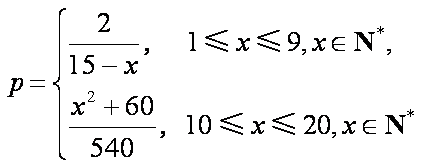

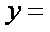
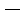
(1)将该车间日利润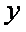
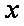
(2)当该车间的日产量为多少件时,日利润最大?最大日利润是几千元?
正确答案
见解析。
解析
(1)由题意可知,
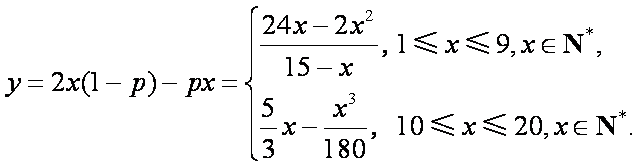
(2)考虑函数
当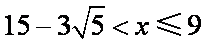
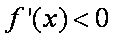
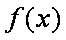
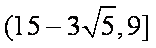
所以当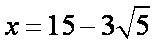
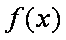
又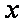
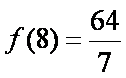
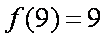
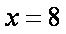
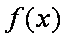
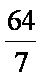
当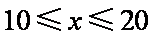
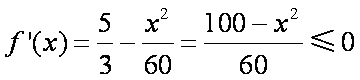

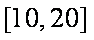
所以当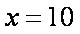
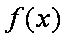

由于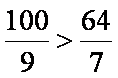
答:当该车间的日产量为10件时,日利润最大,最大日利润是
知识点
如图,在一不规则区域内,有一边长为1米的正方形,向区域内随机地撒1 000颗黄豆,数得落在正方形区域内(含边界)的黄豆数为375颗,以此实验数据为依据,可以估计出该不规则图形的面积为________平方米。
正确答案
解析
设该不规则图形的面积为


知识点
已知

考察下列结论:①



正确答案
解析
∵f(0)=f(0•0)=0,f(1)=f(1•1)=2f(1),∴f(1)=0,①正确;
f(1)=f[(-1)•(-1)]=-2f(-1),∴f(-1)=0,f(-2)=f(-1×2)=-f(2)+2f(-1)=-2≠f(2),
故f(x)不是偶函数,故②错;则f(2n)=f(2•2n-1)=2f(2n-1)+2n-1f(2)=2f(2n-1)+2n,
∴bn=bn-1+1,∴{bn}是等差数列,④正确;b1═1,bn=1+(n-1)×1=n,f(2n)=2nbn=n2n,an═2n,故数列{an}是等比数列,③正确。故答案为:①③④
知识点
扫码查看完整答案与解析