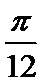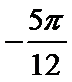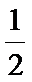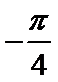- 三角函数的综合应用
- 共157题
14.sin25°+cos235°+sin 5°cos 35°=_______。
正确答案
解析
设M=sin25°+cos235°+sin 5°cos 35°,
配凑一个对偶式N=cos25°+sin235°+cos 5°sin 35°,
则
即
解得M=

知识点
8.已知下列结论:
①若a>|b|,则a2>b2;
②若a>b,则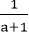
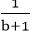
③若a<b,则(

④若a<0,-1<b<0,则ab4>a.
其中正确的是________(只填序号即可)
正确答案
①④
解析
①正确,因为a>|b|≥0,所以a2>b2;
②错误,当a=1,b=-2时,显然不正确;
③错误,因为y=(


④正确,因为a<0,-1<b<0,ab4-a=a(b4-1)>0
所以ab4>a.综上所述,正确的是①④.
知识点
9.已知

正确答案
解析
等式



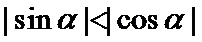

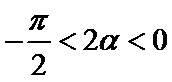
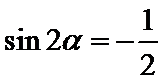
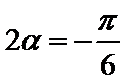
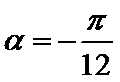
考查方向
解题思路
先把等式两边进行平方,得到
易错点
不能根据三角函数值确定角的范围,或当得到三角函数值时,不能根据角的范围确定角的大小。
知识点
2.
正确答案
解析
由半角公式知
考查方向
解题思路
直接利用辅助角公式即可求值。
易错点
对半角公式不熟悉导致出错。
知识点
10.已知

正确答案

解析

所以
考查方向
解题思路
本题主要考查三角函数的基本性质,诱导公式,两角和与差三角函数,三角函数的恒等变换.解题步骤如下:
把未知角变换成已经角。
利用诱导公式和同角三角函数的基本关系式求解。
易错点
本题不容易想到角的变换,有时公式记错,导致结果错误。
知识点
5.已知函数
正确答案
解析
因为
故选(C)
考查方向
解题思路
由于给出的三角函数不是标准的结构形式
易错点
1、本题易在三角变换时发生错误 。2、记不住倍角公式,导致题目无法进行。
知识点
10.已知函数


正确答案
解析







考查方向
解题思路
由A∩B=A知
易错点
相关知识点不熟悉导致出错。
知识点
4.使函数


正确答案
考查方向
解题思路
本题考查三角函数的图象与性质,解题步骤如下:
由题可知, 

故需要

A选项不正确,C选项不正确,D选项不正确,所以选B选项。
易错点
本题易在公式化简上发生错误。
知识点
5.已知函数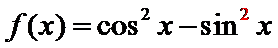
正确答案
解析
因为
故选(C)
考查方向
解题思路
由于给出的三角函数不是标准的结构形式
易错点
1、本题易在三角变换时发生错误 。2、记不住倍角公式,导致题目无法进行。
知识点
9.已知

正确答案
解析
等式









考查方向
解题思路
先把等式两边进行平方,得到
易错点
不能根据三角函数值确定角的范围,或当得到三角函数值时,不能根据角的范围确定角的大小。
知识点
扫码查看完整答案与解析