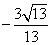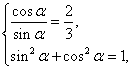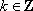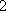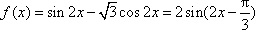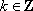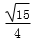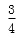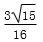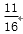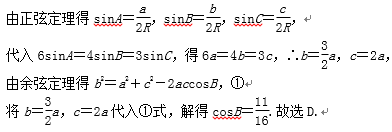- 三角函数的综合应用
- 共157题
已知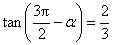
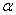
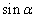
正确答案
解析
由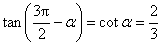
解得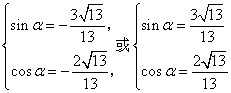
知识点
已知函数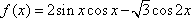
(1)求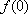
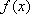
(2)求函数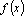
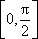
正确答案
(1)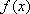
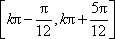
(2)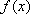
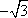
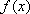
解析
(1)因为
所以,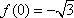
由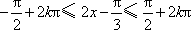
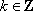
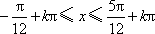
所以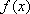
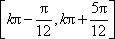
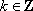
(2)因为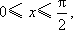
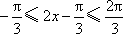
所以,当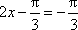
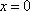
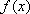
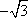
当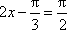
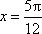

知识点
已知


正确答案
解析
由
解得

知识点
函数
(1)求函数
(2)求函数
正确答案
(1)π
(2)
解析
(1)

(2)由
解得
所以

知识点
函数函数
正确答案
解析
略
知识点
已知

正确答案
解析
略
知识点
某连锁分店销售某种商品,每件商品的成本为



(1)求该连锁分店一年的利润


(2)当每件商品的售价为多少元时,该连锁分店一年的利润

正确答案
见解析。
解析
故
②当







故
答:当

最大值为
当



知识点
已知函数
(1)求
(2)当

正确答案
(1)1
(2)0;
解析
(1)

所以
(2)当

所以,当



当



知识点
已知函数

(1)求函数
(2)若函数

正确答案
(1)
(2)
解析
(1)

∴周期
(2)令

则
因为
所以
所以,若


知识点
若△ABC的内角A、B、C满足6sinA=4sinB=3sinC,则cosB=( )
正确答案
解析
知识点
扫码查看完整答案与解析