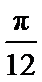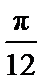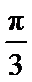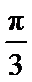三角函数的综合应用_章节学习

1

题型：单选题

|

单选题 · 5 分

6.若将函数y=2sin (2x+)的图像向右平移个周期后,所得图像对应的函数为

Ay=2sin(2x+)

By=2sin(2x+)

Cy=2sin(2x–)

Dy=2sin(2x–)

正确答案

D

解析

考查方向

三角函数图像的平移

解题思路

平移规律：左加右减

易错点

一是平移方向,注意“左加右减“,二是平移多少个单位是对x而言的,不用忘记乘以系数.

知识点

求函数y＝Asin(ωx＋φ)的解析式

1

题型：简答题

|

简答题 · 12 分

在△ABC中，角A，B，C所对的边分别是a，b，c，且。

21.证明：sinAsinB=sinC；

22.若，求tanB。

第(1)小题正确答案及相关解析

正确答案

（Ⅰ）根据正弦定理，可设===k(k>0)．

则a=ksin A，b=ksin B，c=ksin C．

代入+=中，有

+=，变形可得

sin Asin B=sin Acos B+cos Asin B=sin(A+B)．

在△ABC中，由A+B+C=π，有sin(A+B)=sin(π–C)=sin C，

所以sin Asin B=sin C．

解析

（Ⅰ）根据正弦定理，可设===k(k>0)．

则a=ksin A，b=ksin B，c=ksin C．

代入+=中，有

+=，变形可得

sin Asin B=sin Acos B+cos Asin B=sin(A+B)．

在△ABC中，由A+B+C=π，有sin(A+B)=sin(π–C)=sin C，

所以sin Asin B=sin C．

考查方向

本题考查了正弦定理、余弦定理、商数关系、平方关系的知识点。

解题思路

本题考查正弦定理、余弦定理、商数关系等基础知识，考查学生的分析问题的能力和计算能力.在解三角形的应用中，凡是遇到等式中有边又有角时，可用正弦定理进行边角互化，一种是化为三角函数问题，一般是化为代数式变形问题．在角的变化过程中注意三角形的内角和为这个结论，否则难以得出结论．

易错点

本题考查正弦定理、余弦定理、商数关系等基础知识，考查学生的分析问题的能力，在化边为角和化角为边时易错。

第(2)小题正确答案及相关解析

正确答案

（Ⅱ）4.

解析

（Ⅱ）由已知，b2+c2–a2=bc，根据余弦定理，有

cos A==．

所以sin A==．

由（Ⅰ），sin Asin B=sin Acos B+cos Asin B，

所以sin B=cos B+sin B，

故．

考查方向

本题考查了正弦定理、余弦定理、商数关系、平方关系的知识点。

解题思路

本题考查正弦定理、余弦定理、商数关系等基础知识，考查学生的分析问题的能力和计算能力.在解三角形的应用中，凡是遇到等式中有边又有角时，可用正弦定理进行边角互化，一种是化为三角函数问题，一般是化为代数式变形问题．在角的变化过程中注意三角形的内角和为这个结论，否则难以得出结论．

易错点

本题考查正弦定理、余弦定理、商数关系等基础知识，考查学生的分析问题的能力，在化边为角和化角为边时易错。

1

题型：填空题

|

填空题 · 5 分

15.△ABC的内角A，B，C的对边分别为a，b，c，若，，a=1，则b=____________.

正确答案

解析

因为，且为三角形内角，所以，，由正弦定理，所以.

考查方向

正弦定理，三角函数和差公式.

解题思路

在解有关三角形的题目时，要有意识地考虑用哪个定理更适合，或是两个定理都要用，要抓住能够利用某个定理的信息。一般地，如果二次项居多或者三边一角，宜用余弦定理，如果角多宜用正弦定理。在三角形中，任意角的正余弦值转化。

易错点

不能区分正余弦定理应用的环境。

知识点

求函数y＝Asin(ωx＋φ)的解析式

1

题型：单选题

|

单选题 · 5 分

4.要得到函数y=sin(4x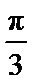－)的图象，只需要将函数y=sin4x的图象（）

A向左平移个单位

B向右平移个单位

C向左平移个单位

D向右平移个单位

正确答案

B

解析

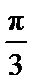
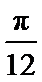
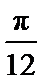
因为y=sin(4x－)=sin4(x－),所以，只需将函数y=sin4x的图象向右平移个单位，故选B.

考查方向

本题考查三角函数图象的变换。

解题思路

应用三角函数图象的变换规则分析求解。

易错点

明确平移的方向和单位数，取决于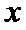加或减的数据.

知识点

求函数y＝Asin(ωx＋φ)的解析式

1

题型：单选题

|

单选题 · 5 分

4、函数(x)=sinx(sinx+cosx)的最大值为（）

A2

B1+

C

D1

正确答案

C

解析

考查方向

本题考察了三角函数最值得求解，利用三角函数倍角公式和辅助角公式进行化简是关键。

解题思路

用三角函数倍角公式和辅助角公式进行化简，再结合三角函数的有界性进行求解即可。

易错点

辅助角公式的符合问题和特殊角问题。

知识点

求函数y＝Asin(ωx＋φ)的解析式

1

题型：单选题

|

单选题 · 5 分

6．已知函数，，下列结论正确的是

A函数与的最大值不同

B函数与在上都为增函数

C函数与的图象的对称轴相同

D将函数的图象上各点的横坐标缩短为原来的，纵坐标不变，再通过平移能得到的图象

正确答案

D

解析

，，所以选择D.

考查方向

简单的三角恒定变换问题。

解题思路

先分别将两个函数化简，然后找到正确答案。

易错点

不记得辅助角公式。

知识点

函数单调性的性质函数奇偶性的性质求函数y＝Asin(ωx＋φ)的解析式

1

题型：单选题

|

单选题 · 5 分

3.函数的部分图像如图所示，则( )

A

B

C

D

正确答案

A

解析

由最高点最低点可知A=2，周期T/2= ,所以把最高点（，2）代入，，故选A。

考查方向

正弦函数图像及性质，考察试图能力。

解题思路

根据图像求解析式问题的一般方法是：先根据图像的最高点、最低点确定A，h的值，由图像找到函数的周期再求ω的值，再根据函数图像上的一个特殊点确定φ值，优先选择最值值点．

易错点

特殊点确定φ值

知识点

求函数y＝Asin(ωx＋φ)的解析式

热门试卷

正确答案

解析

考查方向

解题思路

易错点

知识点

正确答案

解析

考查方向

解题思路

易错点

正确答案

解析

考查方向

解题思路

易错点

正确答案

解析

考查方向

解题思路

易错点

知识点

正确答案

解析

考查方向

解题思路

易错点

知识点

正确答案

解析

考查方向

解题思路

易错点

知识点

正确答案

解析

考查方向

解题思路

易错点

知识点

正确答案

解析

考查方向

解题思路

易错点

知识点